Искусственный интеллект в логистике: реальность или красивые слова?
Л.В. Антонян, А.С. Портнов
Искусственный интеллект для оптимизации управления транспортом и грузоперевозками.
Краткое содержание
1. Общая постановка задачи
2. На практике все еще сложнее
3. Огромный потенциал оптимизации
4. В чём сложность этой задачи?
5. Что же делать?
6. Давайте-ка для начала сходим в горы!
7. А теперь – к бою!
8. Что такое целевая функция и зачем она нужна?
9. Как может выглядеть целевая функция в задаче планирования перевозок?
10. Поиск с запретами в задаче планирования перевозок
11. Так, всё-таки, реальность или красивые слова?
12. Заключение
Вместо введения
Да, есть такое мнение, что никакого искусственного интеллекта вообще не существует, что это всего лишь красивые слова, за которыми стоит вполне естественный интеллект математиков и программистов, вложенный в разработанные ими алгоритмы и программы. В то же время, эти «красивые слова» уже давно у всех на слуху.… Но мы, не углубляясь в дискуссию о терминах, расскажем лучше о нашем собственном опыте разработки, скажем так, «умных» алгоритмов планирования транспортно-логистических процессов, а об их «искусственной интеллектуальности» читатель уж пусть судит сам.
Оговоримся сразу, что речь не будет идти о беспилотных транспортных средствах, роботизированных складах и прочей чудо-технике: пусть ею, как и прежде, пока управляют живые люди, либо беспилотные программно-аппаратные средства. Но даже когда эта «чудо-техника» будет работать без «пилотов», цели ей, в конечном счёте, всё равно должен будет кто-то ставить. И наша задача сделать РОБОТА-ДИСПЕТЧЕРА (или ЛОГИСТА) - мощного, быстрого, безошибочно работающего и не испытывающим усталости и стрессов помощника человека!
На первом этапе наша задача – обеспечивать возможность нажатием кнопки составлять расписание для выполнения заданного объема перевозок: кто, когда, откуда и куда поедет, что и в каких количествах повезёт, где и как загрузится и разгрузится, чтобы в итоге как можно эффективнее выполнить задачи по перевозке грузов. Иными словами, речь в данном случае пойдёт об автоматизации интеллектуального планирования грузоперевозок, хотя это могла быть и перевозка людей, и даже планирование производства, но в этот раз мы для определённости остановимся именно на грузоперевозках.
1. Общая постановка задачи
Имеется один или несколько пунктов отгрузки (производства и/или хранения), пунктов доставки грузов и парк транспортных средств (ТС, от нескольких десятков до нескольких сотен, разной грузоподъемности и вместимости) для перевозки грузов (с разными условиями перевозки) из пунктов отгрузки в пункты доставки. При этом рейсы ТС могут быть, вообще говоря, сборными: то есть, к примеру, ТС может, загрузившись в каком-то пункте отгрузки, объехать затем сразу несколько пунктов доставки, и таких сборных рейсов у каждого ТС в течение заданного планового периода (даже одной смены) может быть несколько.
Собственно, задача состоит в том, чтобы составить план перевозок, то есть «разбросать» требуемые объёмы доставки грузов по имеющемуся парку ТС и построить маршруты и графики движения по ним таким образом, чтобы достичь максимальной экономической эффективности. При этом критерий оптимизации может быть разным – максимальная прибыль, маржа, объем транспортной работы или минимальные затраты, потери, простои, холостые пробеги при соблюдении сроков и ограничений.
Подобные задачи называют - задачей маршрутизации транспорта (в англоязычной литературе – vehicle routing problem). Многие путают данную задачу с задачей коммивояжера - составления оптимального маршрута для отдельных единиц транспорта. Но это не так. Важнейшее отличие в том, что задаче маршрутизации транспорта оптимизируется работа всего парка транспортных средств в целом, а в задаче коммивояжера - оптимизации маршрута отдельных единиц транспорта (как в Яндекс.Навигаторе).
Задача маршрутизации транспорта известна достаточно давно (наверное, уже лет 60), а различные методы её решения появлялись и развивались по мере развития вычислительной техники, так что здесь на лавры первопроходцев мы даже и не претендуем.
2. На практике все еще сложнее
В своей практике мы постоянно сталкиваемся с различными усложнёнными версиями данной задачи, подходы к которым приходилось разрабатывать самостоятельно. Например, в одном из последних проектов таковой оказалась задача планирования перевозок комбикормов с нескольких комбикормовых заводов (ККЗ) на производственные площадки свинокомплексов.
Приведём ряд требований и ограничений, которые необходимо было учесть, чтобы алгоритм планирования перевозок комбикормов был востребован на практике, и которые сделали эту задачу чрезвычайно сложной:
• Несколько источников комбикорма (комбикормовых заводов), и десятки точек доставки (площадок откорма), расположенных в разных точках.
• Многосекционность транспортных средств, которые одновременно могут перевозить несколько марок комбикормов, но при этом корма различных марок должны перевозиться в отдельных секциях;
• Различия комбикормовозов по числу и вместимости секций – в том время как известные алгоритмы решения задачи маршрутизации, как правило, подразумевают, что все ТС одинаковы;
• Необходимость учёта предельно допустимой грузоподъёмности машин и нагрузок на оси;
• Изменение остатков комбикормов на ККЗ, доступных к отгрузке, по мере их производства и отгрузки, что значительно увеличивает вариативность планирования (если к моменту прибытия комбикормовоза на ККЗ кормов, необходимых для его полной загрузки, ещё нет, то можно загрузить его сразу и отправить в пункт назначения недозагруженным, а можно отложить загрузку, что может быть чревато возможной потерей целого рейса из-за нехватки времени в конце смены);
• Необходимость (при планировании маршрутов) учёта так называемой «пирамиды здоровья» (правил биобезопасности): для допуска на площадку с более жёсткими санитарными требованиями (по сравнению с предыдущей) ТС должно пройти специальную санобработку, которая не может быть выполнена на месте;
• Сложные требования (пожелания) свинокомплексов по сочетаниям различных марок комбикормов, доставляемых одним рейсом: это может быть как нежелательность одновременной доставки большого числа различных марок, так и, наоборот, потребность сразу в двух каких-то марках (или более) к заданному моменту времени;
• Множественность окон доставки (разгрузки) комбикормов на каждую из производственных площадок: например, может быть одно окно в начале рабочей смены и одно – в конце;
• Необходимость учёта приоритетности заявок на доставку комбикормов: определённые заявки должны быть выполнены в первоочередном порядке, а исполнение других может быть отложено.
• Многосекционность транспортных средств, которые одновременно могут перевозить несколько марок комбикормов, но при этом корма различных марок должны перевозиться в отдельных секциях;
• Различия комбикормовозов по числу и вместимости секций – в том время как известные алгоритмы решения задачи маршрутизации, как правило, подразумевают, что все ТС одинаковы;
• Необходимость учёта предельно допустимой грузоподъёмности машин и нагрузок на оси;
• Изменение остатков комбикормов на ККЗ, доступных к отгрузке, по мере их производства и отгрузки, что значительно увеличивает вариативность планирования (если к моменту прибытия комбикормовоза на ККЗ кормов, необходимых для его полной загрузки, ещё нет, то можно загрузить его сразу и отправить в пункт назначения недозагруженным, а можно отложить загрузку, что может быть чревато возможной потерей целого рейса из-за нехватки времени в конце смены);
• Необходимость (при планировании маршрутов) учёта так называемой «пирамиды здоровья» (правил биобезопасности): для допуска на площадку с более жёсткими санитарными требованиями (по сравнению с предыдущей) ТС должно пройти специальную санобработку, которая не может быть выполнена на месте;
• Сложные требования (пожелания) свинокомплексов по сочетаниям различных марок комбикормов, доставляемых одним рейсом: это может быть как нежелательность одновременной доставки большого числа различных марок, так и, наоборот, потребность сразу в двух каких-то марках (или более) к заданному моменту времени;
• Множественность окон доставки (разгрузки) комбикормов на каждую из производственных площадок: например, может быть одно окно в начале рабочей смены и одно – в конце;
• Необходимость учёта приоритетности заявок на доставку комбикормов: определённые заявки должны быть выполнены в первоочередном порядке, а исполнение других может быть отложено.
Каких целей позволяет достичь автоматизация планирования перевозок?
Перечислим некоторые из них:
• Существенное повышение качества и одновременно снижение трудоёмкости процесса планирования, включая не только составление самого плана перевозок, но и получение необходимых сопроводительных документов: маршрутных/путевых листов, товарно-транспортных накладных, заданий на отгрузку, экспедирование (в случае необходимости), разгрузку и т.д.;
• Сокращение затрат на содержание и эксплуатацию парка транспортных средств;
• Повышение уровня обслуживания (удовлетворения потребностей) заказчиков доставляемых грузов.
• Существенное повышение качества и одновременно снижение трудоёмкости процесса планирования, включая не только составление самого плана перевозок, но и получение необходимых сопроводительных документов: маршрутных/путевых листов, товарно-транспортных накладных, заданий на отгрузку, экспедирование (в случае необходимости), разгрузку и т.д.;
• Сокращение затрат на содержание и эксплуатацию парка транспортных средств;
• Повышение уровня обслуживания (удовлетворения потребностей) заказчиков доставляемых грузов.
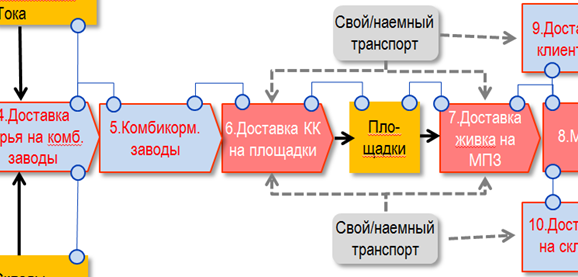
Рисунок 1. Место системы планирования доставки комбикорма (КК) в производственной цепочке агрохолдинга.
3. Огромный потенциал оптимизации в транспортной логистике
Как показывает опыт, если планирование перевозок на предприятии не автоматизировано, то оно максимально упрощено, а управление перевозками происходит в режиме реагирования на текущую ситуацию: при поступлении машин на загрузку вопрос об их отправке в те или иные пункты доставки решается «на лету» путём телефонных переговоров с заказчиками грузов на местах.
При этом руководство пробует вникать в детали процесса только в случае серьезных проблем (существенно превышения транспортного бюджета или срыва производственной программы), т.к. транспортная логистика вещь не простая, и чтобы сделать заключение о правомерности того или иного решения необходимо учесть массу деталей. Поэтому, как правило, возможные издержки покрываются избыточными транспортно-логистическими ресурсами. А требования и/или оправдания логистов-транспортников принимаются на веру.
При таком «планировании» говорить о какой-либо «оптимизации» вообще не приходится. Зато следует говорить о том, что диспетчерам, управляющим процессом, приходится работать в режиме постоянного стресса. В идеале же диспетчер должен лишь контролировать процесс (который за него планирует компьютер), внося необходимые коррективы в нештатных ситуациях: при поломках машин, сбоях в пунктах загрузки или выгрузки и т.д.
И это вполне достижимо – по меньшей мере, процентов на 90-95. Остающиеся 5-10% - это корректировки, которые приходится вносить в план вручную ещё до начала перевозок: всякие нестандартные рейсы, например. Но мы постоянно работаем над сокращением и небольших этих процентов!
Всё вышесказанное свидетельствует о том, что на любом более или менее крупном предприятии обычно имеется огромный потенциал повышения эффективности перевозок: по нашему опыту – от 10 до 25% от текущего транспортного бюджета. Предоставить предприятиям возможность использовать этот потенциал – наша задача.
4. В чём сложность этой задачи?
4. В чём сложность этой задачи?
Однако даже в простейшей постановке (без усложняющих особенностей, подобных вышеперечисленным) задача маршрутизации транспорта весьма небанальна.
Чтобы читатель по-настоящему осознал это, мы приведём своеобразную иерархию разных случаев (в порядке возрастания уровней их сложности).
Однако даже в простейшей постановке (без усложняющих особенностей, подобных вышеперечисленным) задача маршрутизации транспорта весьма небанальна.
Чтобы читатель по-настоящему осознал это, мы приведём своеобразную иерархию разных случаев (в порядке возрастания уровней их сложности).
1. Случай одного ТС, одного пункта отгрузки и одного пункта доставки. В этом случае от задачи маршрутизации не остаётся практически ничего, кроме необходимости построения оптимального маршрута движения между двумя точками, с чем успешно справляют автонавигаторы («Яндекс.навигатор», например). С точки зрения математики, это довольно простая задача. К тому же, особенно актуальна она в городах, где много улиц, перекрёстков, светофоров, где много машин и постоянные пробки. Но комбикорма по городам не возят. А в сельской местности, где относительно немного дорог и машин, оптимальные маршруты обычно известны заранее, да и навигаторы обычно у всех под рукой.… Тем не менее, алгоритм построения оптимального маршрута между двумя точками стоит у нас «на запасном пути». Заметим, однако, что даже в этом варианте нам нужно ещё составлять графики движения ТС по маршруту, а если требуется не один рейс, а несколько, то возникает и вопрос очерёдности вывоза грузов. Но уж, во всяком случае, задача маршрутизации транспорта никак не сводится к построению оптимальных маршрутов между двумя точками, поэтому в дальнейшем во избежание путаницы мы вместо маршрутизации транспорта будем говорить о планировании перевозок.
2. Случай одного ТС, одного пункта отгрузки и нескольких пунктов доставки. Если все грузы можно в этом случае вывезти одним рейсом, то получается так называемая «задача коммивояжёра», состоящая в определении оптимальной очерёдности объезда пунктов доставки. Эта задача уже существенно сложнее первой, а если рейсов требуется несколько – то и подавно.
3. Случай нескольких ТС, нескольких пунктов доставки и нескольких рейсов каждого ТС в течение планового периода. Это и есть полноценная «задача маршрутизации транспорта». И, думается, не надо объяснять, что, даже по сравнению с «задачей коммивояжёра», она неизмеримо сложнее. А ведь есть ещё и масса ограничений (по грузоподъёмности, биобезопасности, окнам доставки и т.д.), которые мы обсуждали выше и которые, прямо скажем, задачу не упрощают…
Тем не менее, если, как говорят математики, размерность задачи мала – скажем, если число используемых транспортных средств (ТС), как и число пунктов отгрузки и доставки, можно сосчитать на пальцах одной руки, - то данная задача теоретически может быть решена полным перебором возможных вариантов. Но на практике, если, допустим, ТС около 10-ти и даже более, а пунктов доставки – хотя бы несколько десятков, то уже даже при одном пункте отгрузки полный перебор за обозримое время становится нереальным (не забываем и о нескольких возможных рейсах каждого ТС в течение планового периода; например, комбикормовозы в рассмотренном выше примере могли даже в течение одной 12-часовой рабочей смены сделать в отдельных случаях до 4-х рейсов).
Именно большая размерность задачи и оказывается той причиной, по которой не только полный перебор, но и такие аналитические методы, как линейное программирование, перестают работать - точнее, оставаясь теоретически применимыми, требуют необозримо большого времени счёта даже на самых мощных компьютерах.
5. Что же делать?
В подобной ситуации многие математики-теоретики скажут, что рассматриваемая задача практически неразрешима. И, на первый взгляд, будут правы. Но в действительности здесь важна постановка задачи. А именно, если требуется найти самое лучшее из всех решений, то есть (в нашем случае) самый оптимальный план перевозок, то да: миссия окажется невыполнимой. Вопрос о том, в каком смысле решение должно быть лучшим, требует отдельного обсуждения, которое мы пока отложим. А сейчас для нас важно, всё-таки, правильно поставить задачу. Так вот, реальная постановка задачи должна состоять в отыскании приемлемого (удовлетворительного) решения. Приемлемого прежде всего, по уровню исполнения заявок на доставку грузов и по транспортным издержкам. Но важно при этом, чтобы решение получалось лучше (или хотя бы не хуже) того, которое в состоянии за разумное время «вручную» найти люди. Хотя на самом деле за несколько секунд (которых нашим программам обычно хватает) люди не в состоянии найти никакого решения, им свойственно ошибаться, их рабочее время, по сравнению с компьютерным, стоит дорого, да и люди сами пользуются теми же компьютерами (обычно прибегая к помощи Excel’а)…
И вот в такой постановке к задаче уже можно подступиться. Некоторые возможные подходы, хорошо известные людям, интересующимся рассматриваемыми вопросами, обсуждаются, например, в нашей статье [1]. Это алгоритм муравьиной колонии, метод генетических алгоритмов, алгоритм имитации отжига и некоторые другие. Они очень разные, каждый по-своему интересен, но есть у них и нечто общее: всё это – так называемые эвристические алгоритмы. Вот вам ещё одно красивое слово, но означает оно очень простую вещь. А именно, что эти алгоритмы не имеют строгого логического обоснования и не гарантируют получения не только лучшего, но и, вообще, какого бы то ни было решения задачи. То есть на вопросы типа: «Почему это работает?» и «Сработает ли в нашем конкретном случае?» не стоит ожидать исчерпывающих ответов. Хотя и находятся любители такие ответы (обычно притянутые за уши) и поискать. Видя, как это загадочным образом и в самом деле работает!
Правда, надо отметить, что все эти самые эвристики, строго говоря, не являются готовыми алгоритмами: это, скорее, общие подходы, методы решения задач, которые в каждом конкретном случае требуют конкретной реализации. И от того, насколько эта реализация окажется удачной, существенно зависит на самом деле и конечный результат. Кроме того, обычно в этих эвристиках есть, как мы увидим далее, различные управляющие параметры, удачный подбор которых тоже крайне важен. Ещё одна особенность эвристических алгоритмов состоит в том, что сами они по себе, даже найдя требуемое решение, обычно не останавливаются, а продолжают упорно пытаться его улучшить (возможно, уже «на копейки»). Для остановки поиска пользователь должен заранее выделять на него определённое компьютерное время, и при этом, в любом случае, чем дольше работает алгоритм, тем, вообще говоря, лучше получается решение. «Вообще говоря» - потому, что он может быстро найти решение, которое в дальнейшем не сможет улучшить. От чего это зависит? От многих факторов: и от постановки задачи и её размерности, и от жёсткости ограничений, и от эффективности алгоритма, и от подбора управляющих параметров.… Но и, конечно, от быстродействия компьютера, на которых алгоритм исполняется.
Но при прочих равных условиях скорость исполнения алгоритма существенным образом зависит ещё и от того, каким образом он запрограммирован и откомпилирован. Мы используем известный язык программирования, который «заточен» как раз под реализацию алгоритмов и который компилируется непосредственно в машинные коды, что обеспечивает максимально возможное быстро¬действие (это вольность речи: на самом деле компилируется написанный на нём программный код).
Кроме того, этот язык жёстко стандартизирован, что облегчает перенос написанных на нём программ на различные платформы. Правда, в настоящее время мы делаем свои разработки исключительно под MS WINDOWS, а алгоритмы реализуем в отдельных динамически подключаемых библиотеках, которые могут вызываться из любых приложений, работающих под управлением WINDOWS. Это «убивает» сразу нескольких «зайцев»:
• Обеспечивает как раз максимальное быстродействие, причём благодаря как вышеупомянутой «заточенности» языка программирования высокого уровня и машинным кодам DLL, так и тому, что при необходимости DLL может вызываться удалённо с любого клиентского терминала, а располагаться и исполняться на сколь угодно мощном сервере;
• Обеспечивает возможность интеграции с корпоративными информационными системами наших заказчиков;
• Упрощает нам разработку новых версий алгоритмов и их ввод в эксплуатацию у заказчиков.
Теперь, пожалуй, уже созрело время рассмотреть какой-нибудь алгоритм более подробно. Но мы приготовили для читателя неожиданный поворот сюжета.
• Обеспечивает как раз максимальное быстродействие, причём благодаря как вышеупомянутой «заточенности» языка программирования высокого уровня и машинным кодам DLL, так и тому, что при необходимости DLL может вызываться удалённо с любого клиентского терминала, а располагаться и исполняться на сколь угодно мощном сервере;
• Обеспечивает возможность интеграции с корпоративными информационными системами наших заказчиков;
• Упрощает нам разработку новых версий алгоритмов и их ввод в эксплуатацию у заказчиков.
Теперь, пожалуй, уже созрело время рассмотреть какой-нибудь алгоритм более подробно. Но мы приготовили для читателя неожиданный поворот сюжета.
6. Давайте-ка для начала сходим в горы!
Кто-то в этом месте скажет, что в горы надо идти хорошо подготовленным, кто-то даже вспомнит знаменитое «Умный в гору не пойдёт…», но мы сразу раскроем карты.
Дело в том, что далее мы собираемся подробно обсудить ещё один эвристический метод – метод направленного поиска с запретами (по-английски – taboo search). По-русски этот метод часто называют поиском с исключениями, а по-английски пишут не taboo, а tabu. Но слово «запрет» несколько короче слова «исключение», да и, на наш взгляд, более адекватно отражает суть дела, а английское слово «tabu» являющееся сокращением от «taboo».
Дело в том, что далее мы собираемся подробно обсудить ещё один эвристический метод – метод направленного поиска с запретами (по-английски – taboo search). По-русски этот метод часто называют поиском с исключениями, а по-английски пишут не taboo, а tabu. Но слово «запрет» несколько короче слова «исключение», да и, на наш взгляд, более адекватно отражает суть дела, а английское слово «tabu» являющееся сокращением от «taboo».
Данный метод ни здесь пока, ни в статье [1] не упоминался (более детальное описание и этого, и многих других алгоритмов подготовленный читатель может найти в работе [2]. Данная наша статья рассчитана на максимально широкую читательскую аудиторию). Чтобы плавно подвести читателя к его пониманию, мы начнём с рассмотрения следующего совсем простого примера.
Пусть некто (назовём его путником) отправляется в горы с целью найти там самую высокую вершину. При этом будем предполагать, что наш путник «видит» только на один шаг вперёд. Точнее, что, находясь в любом месте, он может судить, куда – в зависимости от выбора направления – поведёт его следующий шаг: вверх или вниз и на сколько именно сантиметров он в результате поднимется либо опустится. Это важно для того, чтобы в любой момент путник знал высоту своего текущего местоположения и мог сравнить её с высотой ранее достигнутых вершин (точнее, самой высокой из них).
…Хм… нелегко придётся нашему незрячему путнику в горах, да и по какой-нибудь отвесной скале не очень-то и походишь…. Поэтому пусть это лучше будут не горы, а холмы – с мягкими, пологими склонами…
Итак, наш путник стартует из какой-нибудь начальной точки где-то в долине. От этой точки ему логично будет в дальнейшем отсчитывать высоту своего текущего местонахождения (это будет, скажем так, «высота над уровнем долины»). Соответственно, в начальной точке высота местонахождения h0 = 0. Тогда высота после первого шага будет равна:
Итак, наш путник стартует из какой-нибудь начальной точки где-то в долине. От этой точки ему логично будет в дальнейшем отсчитывать высоту своего текущего местонахождения (это будет, скажем так, «высота над уровнем долины»). Соответственно, в начальной точке высота местонахождения h0 = 0. Тогда высота после первого шага будет равна:
h1 = h0 + Δh1 ,
где Δh1 – то самое изменение высоты, которое наш путник в состоянии измерить (по-математически – приращение. Термин «приращение» применяется независимо от знака соответствующей величины, то есть и в тех случаях, когда это самое «приращение» равно нули или отрицательно). Аналогично, после второго шага высота станет равной:
h2 = h1 + Δh2 ,
где Δh2 – приращение уже на 2-м шаге, и т.д. Например, если 1-й шаг будет сделан в горизонтальном направлении, то будем иметь Δh1 = 0 и h1 = 0 + 0 = 0. Далее, если на 2-м шаге произойдёт подъём на 15 см, то есть на 0,15 м, то после этого шага путник окажется на высоте
h2 = 0 + 0,15 = 0,15 м.
Если затем придётся сделать шаг вниз, допустим, на 5 см, то после этого (уже 3-го) шага высота составит
h3 = 0,15 + (-0,05) = 0,1 м.
h2 = 0 + 0,15 = 0,15 м.
Если затем придётся сделать шаг вниз, допустим, на 5 см, то после этого (уже 3-го) шага высота составит
h3 = 0,15 + (-0,05) = 0,1 м.
Тем самым, путник в любой момент будет знать, на какой высоте он находится.
Но какой стратегии следует придерживаться этому нашему путнику? Наверное, логично всё время стремиться вверх, делая каждый очередной шаг в направлении наиболее крутого подъёма. Но к чему приведёт такая стратегия? Очевидно, к тому, что путник взберётся на какой-нибудь ближайший холм (а возможно, это даже будет и вовсе кочка, как это и случилось в приведённом выше примере) и сочтёт цель достигнутой: ведь он не может видеть других, более высоких холмов. Математик назовёт эту ситуацию ловушкой локального экстремума (в нашем случае – максимума): ведь все дальнейшие пути ведут только вниз, а значит, максимум достигнут – но, увы, именно лишь локальный…
Но какой стратегии следует придерживаться этому нашему путнику? Наверное, логично всё время стремиться вверх, делая каждый очередной шаг в направлении наиболее крутого подъёма. Но к чему приведёт такая стратегия? Очевидно, к тому, что путник взберётся на какой-нибудь ближайший холм (а возможно, это даже будет и вовсе кочка, как это и случилось в приведённом выше примере) и сочтёт цель достигнутой: ведь он не может видеть других, более высоких холмов. Математик назовёт эту ситуацию ловушкой локального экстремума (в нашем случае – максимума): ведь все дальнейшие пути ведут только вниз, а значит, максимум достигнут – но, увы, именно лишь локальный…
Но будем считать, что наш путник, всё-таки, заподозрит, что где-то дальше, возможно, есть более высокие холмы, и поэтому продолжит своё движение. Куда? С неизбежностью вниз, поскольку никаких путей вверх на данный момент нет. Только вниз он будет стремиться двигаться уже не по самому крутому, а по самому пологому склону, чтобы по возможности меньше терять высоту. Но с соблюдением важного правила запретов: не возвращаться туда, откуда пришёл, чтобы, как говорят программисты, не «зацикливаться». Причём заметим, что после первого же шага с достигнутой вершины вниз первоначальная стратегия (стремиться всё время вверх) могла бы заставить путника сразу же вернуться назад (если бы не было другого, причём более крутого пути вверх), но правило запретов этому воспрепятствовало бы. Однако это правило не должно действовать вечно, поскольку в каком-то месте своего маршрута наш путник мог пройти мимо какой-нибудь перспективной тропинки. Да и память человека, как принято говорить, «не резиновая».… Поэтому надо позволить нашему путнику возвращаться в ранее пройденные точки маршрута, но не сразу, а через определённое число (например, 100) шагов, называемое в этой науке длиной списка запретов (исключений).
Кроме того, правило запретов может нарушаться, если это ведёт к достижению нового рекорда (в нашем случае – высоты подъёма). Правда, в этом нашем простом примере подобное невозможно, но дело в том, что на практике правило запретов выглядит чуть иначе, чем у путника. Потому что практически нереально в точности запоминать все пункты маршрута (а в дальнейшем это у нас будут планы перевозок); реально фиксировать только какие-то характерные признаки, которые могут и повторяться (подробнее обсудим этот аспект ниже).
Вот, собственно, и вся стратегия: стараться всё время подниматься вверх, причём как можно быстрее (по самому крутому пути), а если вверх не получается, то спускаться вниз как можно медленнее и при этом всё время соблюдать правило запретов. И всякий раз по достижении новой (более высокой, чем ранее) вершины запоминать её местоположение и высоту как результат поиска (вместо предыдущего). Конечно, ходить так можно бесконечно долго, поэтому нужно заранее ограничить либо время поиска, либо число шагов. Как вариант, можно ограничивать число неудачных шагов – точнее, число шагов после последнего рекордного результата (наилучшего решения), но в таком варианте время поиска может оказаться непредсказуемо (и неприемлемо) большим.
7. А теперь – к бою!
А теперь мы обсудим пример практического применение описанного выше метода (поиска с запретами). В нашей практике таких задач было три: в одном случае это было планирование производства (а, конкретно – стеклотары), а в двух других – планирование перевозок. Для определённости мы возьмём задачу планирования развоза комбикормов, постановка которой уже обсуждалась выше.
С первого взгляда, аналогию с хождением путника по горам увидеть трудно: там путник был всего один, а здесь машин много; там целью перемещений путника было достичь заранее не известной (самой высокой) точки, а здесь все точки известны, а перемещения между ними имеют целью доставку грузов из одних в другие. В общем, вроде и в самом деле – ничего общего. Но по ходу нашего дальнейшего повествования аналогия проступит сама собой.
Прежде всего, аналогом пункта маршрута путника по горам и долам будет план перевозок. Причём, отметим, не отдельный рейс и даже не целая смена отдельной машины, а все рейсы всех машин вместе, причём начиная с выдачи путевых листов в начале смены, включая погрузо-разгрузочные операции (и, разумеется, движение по маршрутам) и заканчивая сдачей путевых листов! И точно так же, как путник обходил различные точки местности, умный планировщик «обходит» различные планы перевозок, но не хаотично и не перебирая все возможные варианты подряд, а, как и путник, следуя определённой стратегии. На самом деле – той же стратегии, что и путник, но перенесённой на гораздо более содержательную и сложную задачу. Как именно – станет ясно чуть позже, а пока обсудим одно важное понятие.
8. Что такое целевая функция и зачем она нужна?
Давайте вспомним, что наш путник, блуждая по местности, постоянно контролировал высоту своего местоположения – с тем, чтобы, взобравшись на очередную вершину, иметь возможность сравнить её с самой высокой из ранее покорённых вершин именно по высоте. Ведь его целью был поиск именно самой высокой вершины! А в математических терминах получается так: в решавшейся путником задаче оптимизации высота была целевой функцией – как переменная (зависящая от местоположения - фактически это функция двух (независимых) переменных: широты и долготы точки местности) величина, подлежащая (в данном случае) максимизации.
Таким образом, целевая функция определяет критерий выбора оптимального (наилучшего) из всех допустимых решений (в случае с путником – самой высокой из всех точек местности). Но этим её роль в стратегии поиска с запретами не исчерпывается, поскольку она (вернее, её возможные приращения) используется на каждом шаге процесса поиска при выборе направления дальнейшего движения. Причём заметим, что если бы путник, придерживаясь какой-то другой стратегии, не рассчитывал (через приращения) величину целевой функции на каждом шаге своего движения, то, достигнув вершины, он должен был бы каким-то иным способом определить её высоту, что, скорее всего, оказалось бы для него вообще непосильной задачей.
9. Как может выглядеть целевая функция в задаче планирования перевозок?
Давайте на эту тему немного порассуждаем.
В задаче планирования перевозок целевая функция должна играть абсолютно ту же роль, что и в примере с путником: позволять сравнивать разные планы перевозок и определять, который из них лучше. Но что значит «лучше»? В каком смысле? В случае с путником всё было просто: «лучше» означало «выше». Но в задаче планирования перевозок всё намного сложнее.
В задаче планирования перевозок целевая функция должна играть абсолютно ту же роль, что и в примере с путником: позволять сравнивать разные планы перевозок и определять, который из них лучше. Но что значит «лучше»? В каком смысле? В случае с путником всё было просто: «лучше» означало «выше». Но в задаче планирования перевозок всё намного сложнее.
Для определённости снова вернёмся к задаче развоза комбикормов с одного (для простоты) комбикормового завода на несколько площадок свинокомплексов.
В простейшем случае – при заданных фиксированных объёмах перевозок – в качестве целевой функции можно взять затраты на перевозку (и их, естественно, минимизировать). Но здесь сразу возникают, по меньшей мере, два возражения. Во-первых, сплошь и рядом случается так, что доставить заказанные свинокомплексами корма в полном объёме имеющимся парком автотранспорта попросту невозможно. В такой ситуации неизбежно возникают недопоставки, причём понятно, что меры по их недопущению (это может быть довоз в сверхурочное время, наём стороннего транспорта и т.д.) наверняка потребуют увеличения затрат, в результате чего доставленные корма могут, образно выражаясь, стать «золотыми»!
Возможным ответом на это возражение является добавление в целевую функцию штрафов за недопоставки. Как эти штрафы считать – отдельный вопрос, к которому мы ещё вернёмся. А пока что отметим, что в идеале штрафы за недопоставку должны быть разными не только для разных площадок, но и для разных заявок на доставку кормов, поскольку степень критичности недопоставок может в разных случаях быть разной. Как вариант (также реализованный в нашем алгоритме), можно различать заявки по уровням срочности (приоритетности) доставки и для каждого уровня предусматривать свои размеры штрафов. Кроме того, штрафы могут быть (и также предусмотрены в нашем алгоритме) не только за недопоставки: например, может штрафоваться (но не всегда и не везде!) доставка большого числа (даже двух) разных марок кормов одним рейсом, поскольку это ведёт к существенному увеличению продолжительности разгрузки ТС на площадке свинокомплекс (да и загрузки тоже, поскольку загрузка каждой марки корма сопровождается взвешиванием ТС).
Но и со штрафами целевая функция сохраняет определённые недостатки. Дело в том, что, наряду с недопоставками, бывают, напротив, авансовые поставки в счёт будущих потребностей.
Например, если переменные транспортные затраты на идеальный рейс оказались равными 3200 руб., а заданная наценка была 25%, то здесь получится: 3200 × (1 + 0,25) = 4000 руб. Тогда при грузоподъёмности ТС, равной (для ровного счёта) 20 т, тариф на доставку тонны кормов на рассматриваемую площадку составит: 4000 / 20 = 200 руб./т.
Конечно, при наличии на местах свободных бункеров для приёма кормов. Вообще, ёмкостей для хранения кормов часто не хватает и на свинокомплексах, и на комбикормовых заводах. А на ККЗ – ещё и производственных мощностей, поэтому там стремятся как можно реже менять марки производимых кормов, поскольку переналадки оборудования приводят к потере производительности. По этим причинам перманентно возникают перекосы между наличием кормов на ККЗ и потребностями свинокомплексов: когда при нехватке одних кормов другие оказываются в избытке, а бункеры ККЗ - переполнеными. Если в таких условиях корма вывозятся с ККЗ на свинокомплексы строго по их текущим заявкам, то машины часто ездят недогруженными, что только усугубляет ситуацию. Необходимую для освобождения бункеров ККЗ и дозагрузки комбикормовозов свободу манёвра и обеспечивают авансовые поставки.
Помимо того, что свинокомплексам такие поставки обеспечивают определённую страховку от недопоставок в ближайшем будущем, комбикормовому заводу они позволяют избежать остановок производства из-за переполнения бункеров с готовой продукцией. Но при той структуре целевой функции, на которой мы пока остановились (затраты на доставку кормов плюс штрафы), наш алгоритм заведомо не будет планировать никаких авансовых поставок, поскольку они требуют дополнительных затрат, а штрафы за их неисполнение выглядели бы противоестественно (и, не исключено, приводили бы к противоестественным результатам).
Поэтому надо пойти ещё чуть дальше.
Представим себе (если на самом деле это не так), что автотранспортное предприятие (АТП), перевозящее корма, является, как и ККЗ, и свинокомплексы, самостоятельным хозяйствующим субъектом. Тогда мы сразу увидим, чего не хватает в нашей целевой функции. Ведь и затраты на перевозку, и штрафы – это для АТП одни издержки, а где же доходы? Доходы АТП – это оплата его услуг по перевозке грузов. Но по каким тарифам?
Представим себе (если на самом деле это не так), что автотранспортное предприятие (АТП), перевозящее корма, является, как и ККЗ, и свинокомплексы, самостоятельным хозяйствующим субъектом. Тогда мы сразу увидим, чего не хватает в нашей целевой функции. Ведь и затраты на перевозку, и штрафы – это для АТП одни издержки, а где же доходы? Доходы АТП – это оплата его услуг по перевозке грузов. Но по каким тарифам?
Единый тариф за тонно-километр здесь не очень подходит, поскольку существенную роль играют здесь технологические простои, в частности, обусловленные необходимостью соблюдения жёстких санитарных требований: на санобработку комбикормовоза в АТП и его дезинфекцию перед въездом на площадки свинокомплексов может за смену уйти не один час времени. Поэтому имеет смысл отдельно учитывать пробег и общее время использования ТС (по покилометровому и почасовому тарифам соответственно). А поскольку при этом будет учтена только часть затрат (причём только переменных) на перевозки комбикормов (к тому же, не все реальные рейсы будут получаться «идеальными»), да и какая-то прибыль у АТП ведь тоже должна оставаться, то на эти затраты надо ещё «накинуть» наценку (которую мы называем также маржинальной рентабельностью перевозок). Именно так и делается в нашем алгоритме: непосредственному планированию перевозок предшествует их тарификация.
Делается это следующим образом. Для каждой из производственных площадок свинокомплексов (на которые требуется доставлять корма) рассматривается, как мы его называем, «идеальный рейс» с комбикормового завода на площадку и обратно, включая все требуемые операции (которые для этого заранее нормируются): оформление документов и взвешивание пустого ТС на ККЗ, полную загрузку ТС одной маркой комбикорма (поскольку в таком случае как загрузка, так и последующая разгрузка ТС на площадке происходят максимально быстро), взвешивание загруженного ТС, движение ТС с ККЗ на площадку, взвешивание и дезинфекцию ТС перед въездом на площадку, разгрузку ТС и возвращение его на ККЗ. Общая продолжительность и километраж «идеального рейса» умножаются на заданные почасовой и покилометровый тарифы за использование ТС соответственно, полученные произведения суммируются, результат (переменные транспортные затраты на рейс) увеличивается на заданную (в процентах) величину наценки и делится на грузоподъёмность ТС.
Например, если переменные транспортные затраты на идеальный рейс оказались равными 3200 руб., а заданная наценка была 25%, то здесь получится: 3200 × (1 + 0,25) = 4000 руб. Тогда при грузоподъёмности ТС, равной (для ровного счёта) 20 т, тариф на доставку тонны кормов на рассматриваемую площадку составит: 4000 / 20 = 200 руб./т.
В итоге получается тариф на доставку тонны комбикорма на данную конкретную площадку. К этим тарифам, в свою очередь, привязываются штрафы. В частности, штраф за недопоставку задаётся в процентах от тарифа на доставку.
Например, если тариф на доставку кормов на какую-то площадку был, как выше, 200 руб./т, штраф за недопоставку – 80% от этого тарифа, а фактическая недопоставка на данную площадку составила 5 т, то штраф за эту недопоставку составит: (200×0,8) × 5 = 800 руб., где в скобках – штраф за недопоставку 1-й тонны.
Новая целевая функция будет выглядеть тогда следующим образом. Это будет маржинальная прибыль (МП) рассматриваемого плана перевозок, рассчитываемая как выручка (В) за вычетом затрат (З) и штрафов (Ш):
МП = В – З – Ш . (1)
При этом выручка В рассчитывается как сумма произведений (по площадкам) объемов (тоннажа) запланированных перевозок комбикормов на те самые предварительно рассчитанные тарифы, затраты З – как сумма произведений продолжительности и километража всех рейсов, входящих в план, на по почасовой и покилометровый тарифы соответственно, а штрафы также суммируются по всему плану перевозок.
МП = В – З – Ш . (1)
При этом выручка В рассчитывается как сумма произведений (по площадкам) объемов (тоннажа) запланированных перевозок комбикормов на те самые предварительно рассчитанные тарифы, затраты З – как сумма произведений продолжительности и километража всех рейсов, входящих в план, на по почасовой и покилометровый тарифы соответственно, а штрафы также суммируются по всему плану перевозок.
В план входят также необходимые операции перед выездом ТС из АТП в начале смены (выдачу путевого листа и др.), движение ТС из АТП на ККЗ, а также возвращение ТС в АТП и необходимые операции (в частности, мойку ТС и сдачу путевого листа водителем) в конце смены. То есть, подчеркнём, речь здесь уже идёт не об «идеальных», а о реальных рейсах.
Естественно, теперь целевая функция подлежит уже не минимизации, а максимизации.
Отметим, что в нашу новую целевую функцию входит целый ряд коэффициентов, в частности, наценка (маржинальная рентабельность перевозок) и ставки штрафов, варьируя которые, можно менять стратегию планирования в зависимости от того, что для нас важнее. Например,
• Если важнее увеличивать загрузку ТС (и, тем самым, уменьшать затраты на перевозку и количество используемых единиц транспорта), то надо снижать наценку (снижение наценки ведёт к снижению тарифов, вследствие чего недозагруженные рейсы становятся нерентабельными и в план перевозок не попадают);
• Если важнее снижать недопоставки, то надо увеличивать ставку штрафа за недопоставки.
Отметим, что в нашу новую целевую функцию входит целый ряд коэффициентов, в частности, наценка (маржинальная рентабельность перевозок) и ставки штрафов, варьируя которые, можно менять стратегию планирования в зависимости от того, что для нас важнее. Например,
• Если важнее увеличивать загрузку ТС (и, тем самым, уменьшать затраты на перевозку и количество используемых единиц транспорта), то надо снижать наценку (снижение наценки ведёт к снижению тарифов, вследствие чего недозагруженные рейсы становятся нерентабельными и в план перевозок не попадают);
• Если важнее снижать недопоставки, то надо увеличивать ставку штрафа за недопоставки.
Отметим также, что хотя и целевая функция (1) имеет понятный экономический смысл, использовать её в алгоритме планирования не совсем удобно. Потому что в нём процесс планирования стартует с пустого плана перевозок (в котором нет ни одного рейса). Рейсов нет, а штрафы-то есть! В частности, штраф за недопоставку максимален! И, главное, подлежит расчёту!
К счастью, однако, этого можно избежать, если увеличить целевую функцию на величину этого начального штрафа – так, чтобы начальное значение целевой функции было нулевым. Как, кстати, было и в примере с путником в горах. Ведь там мы тоже условились отсчитывать высоту не от уровня моря, а от стартовой точки маршрута путника в долине. Поэтому и здесь мы возьмём старт с нулевой отметки и будем, как и там, отслеживать приращения целевой функции. Соответственно, наша целевая функция (ЦФ) будет иметь следующий окончательный вид:
ЦФ = В – З – Ш’, (1)
где Ш’ = Ш – Ш0 , а Ш0 – начальное значение суммарного штрафа (когда план перевозок пуст).
ЦФ = В – З – Ш’, (1)
где Ш’ = Ш – Ш0 , а Ш0 – начальное значение суммарного штрафа (когда план перевозок пуст).
Вообще, это, конечно, детали, чисто математические штучки, но кому-то из читателей они, возможно, могли быть любопытны… Пора, однако, двигаться дальше.
10. Поиск с запретами в задаче планирования перевозок
Сейчас мы в общих чертах обсудим практическое применение метода направленного поиска с запретами (на примере всё того же развоза комбикормов). При этом будем постоянно апеллировать к аналогии с путником, блуждающим по холмам и долинам.
Итак, путник стартовал из начальной точки внизу, в долине. Мы стартуем с пустого плана перевозок.
Путник шагал из одной точки местности в другую. Мы будем «шагать» от одного плана перевозок к другому.
Путник стремился подниматься вверх, но иногда ему приходилось спускаться вниз. Для нас «подниматься вверх» будет означать добавлять в план производства один новый рейс, а «опускаться вниз» - удалять из плана один из ранее добавленных рейсов.
Путник шагал из одной точки местности в другую. Мы будем «шагать» от одного плана перевозок к другому.
Путник стремился подниматься вверх, но иногда ему приходилось спускаться вниз. Для нас «подниматься вверх» будет означать добавлять в план производства один новый рейс, а «опускаться вниз» - удалять из плана один из ранее добавленных рейсов.
При этом путник был вообще совсем один, а машин, которым можно добавлять и удалять рейсы – несколько. Так что здесь уже возникают варианты. Правда, путник тоже выбирал направление движения, но здесь выбор получается множественным: сначала надо выбрать машину, потом (при добавлении рейса) – площадку, на которую она поедет, потом – когда именно поедет. Потому что – на этом важно сделать акцент – имеет смысл рассматривать добавление рейса не только в конец смены, то есть после последнего из ранее добавленных, но и в начало или в середину (то есть между ранее добавленными). И только потом нужно загружать комбикормовоз кормами, потому что это будет зависеть и от его вместимости по секциям, и от потребности (причём с учётом ранее запланированных рейсов) выбранной площадки в кормах, и от наличия кормов на ККЗ на момент загрузки…
Путник выбирал направление каждого своего следующего шага очень просто (правило запретов пока не вспоминаем): чтобы максимально круто подниматься вверх, что давало максимальный прирост целевой функции. У путника таковой была высота местонахождения, так что ему было сравнительно просто. У нас теперь целевая функция гораздо сложнее, но и мы можем посчитать её приращения для всех возможных вариантов добавления рейса и выбрать из них самый «крутой». На первых шагах это будут, скорее всего, самые дальние рейсы, но потом они могут из плана уйти, поскольку может оказаться, что, к примеру, вместо одного длинного рейса предпочтительнее два более коротких. Или вместо двух – три, или вместо трёх – четыре…. Но это будет потом. А пока путник поднимается всё выше и выше, мы добавляем в наш план перевозок один рейс за другим…
Но вот путник достиг вершины, а мы, соответственно, столкнулись с невозможностью дальнейшего добавления рейсов. Тогда путник будет вынужден сделать шаг вниз, а мы – удалить из плана один из рейсов. Чтобы потом, как и путник, поискать другие варианты. Путник запомнил достигнутую вершину и её высоту, и мы, в свою очередь, занесли в «память» нашей процедуры планирования полученный план перевозок вместе с рекордным на данный момент значением целевой функции.
И вот здесь пора вспомнить о правиле запретов. Мы предполагали, что путник, чтобы не возвращаться назад, будет запоминать раннее пройденные места – по крайней мере, будет помнить последние несколько десятков или сотню-другую шагов. Наверное, для этого потребовалась бы очень хорошая память. Но нам-то сейчас (с кормами) надо запоминать целые планы перевозок, состоящие из десятков рейсов! В мельчайших подробностях! А потом сравнивать их с новыми! Представляете себе: пришлось бы на каждом шаге, получив новый план, сравнить его с доброй сотней ранее запомненных планов, каждый из которых состоит из десятков рейсов! А потом и сам этот план запомнить! Тут любой программист сразу скажет, что подобное возможно лишь теоретически, а практически нереально! Если, конечно, мы хотим сделать не сотню-другую шагов, а на порядки больше.
К счастью, в том, о чём говорится в предыдущем абзаце, нет необходимости. Запоминать полностью надо только «рекордные» планы, то есть те, которые улучшают ранее достигнутые наилучшие значения целевой функции. В частности, если рассматривать наш итерационный процесс планирования с самого первого шага, то необходимость запоминания решения первый раз возникнет только при достижении первой «вершины», то есть на том шаге, когда добавление новых рейсов станет невозможным. А в следующий раз – по достижении более высокой «вершины» (если такое вообще случится).
А для правила запретов мы использовали следующую схему, которую опишем, не вдаваясь в детали.
• Если на i-том шаге (i = 1, 2, 3, …) описанного выше итерационного процесса планирования в план перевозок добавляется новый рейс, то номер i запоминается в специальном атрибуте рейса (как номер шага, на котором этот рейс попал в план), чтобы на протяжении какого-то числа шагов (которое будем называть длиной списка запретов на удаление рейсов) правило запретов препятствовало удалению этого рейса из плана;
• Если же на i-том шаге того же итерационного процесса из плана перевозок удаляется рейс ТС с порядковым номером v (v = 1, 2, …, V, где V – число ТС) в пункт доставки (на площадку свинокомплекса) с порядковым номером p (p = 1, 2, …, P, где P – число площадок), то номер i запоминается в специальном двумерном массиве (как номер шага, на котором рейс был удалён), чтобы на протяжении какого-то числа шагов (которое будем называть длиной списка запретов на добавление рейсов) правило запретов препятствовало добавлению в план перевозок рейса v-того ТС на p-тую площадку, если такое добавление не приводит к большему, по сравнению с предыдущими (то есть «рекордному»), значению целевой функции.
• Если на i-том шаге (i = 1, 2, 3, …) описанного выше итерационного процесса планирования в план перевозок добавляется новый рейс, то номер i запоминается в специальном атрибуте рейса (как номер шага, на котором этот рейс попал в план), чтобы на протяжении какого-то числа шагов (которое будем называть длиной списка запретов на удаление рейсов) правило запретов препятствовало удалению этого рейса из плана;
• Если же на i-том шаге того же итерационного процесса из плана перевозок удаляется рейс ТС с порядковым номером v (v = 1, 2, …, V, где V – число ТС) в пункт доставки (на площадку свинокомплекса) с порядковым номером p (p = 1, 2, …, P, где P – число площадок), то номер i запоминается в специальном двумерном массиве (как номер шага, на котором рейс был удалён), чтобы на протяжении какого-то числа шагов (которое будем называть длиной списка запретов на добавление рейсов) правило запретов препятствовало добавлению в план перевозок рейса v-того ТС на p-тую площадку, если такое добавление не приводит к большему, по сравнению с предыдущими (то есть «рекордному»), значению целевой функции.
Таким образом, правило запретов у нас получилось более сложным, чем у путника: у него был всего один параметр L – длина списка запретов и один собственно список запретов – перечень мест, в которые нельзя возвращаться на следующем шаге. Например, если L = 1, то, делая любой шаг, путник должен лишь помнить, что следующий шаг нельзя будет сделать назад, если L = 2, то надо помнить ещё и предыдущее место (куда тоже нельзя будет на следующем шаге вернуться) и так далее. А если путник зашёл в тупик, из которого только один выход – назад? Понятно, что в этом случае, чтобы не останавливаться, ему, всё-таки, придётся нарушить правило запретов, причём даже при L = 1! И это только одна из проблем!
Первая проблема возникает ещё до того, как наш путник отправится в путь: какой вообще должна быть длина списка запретов L? Понятно, что чем она меньше, тем больше у путника свободы выбора каждого следующего шага, но и тем больше возможностей «зациклиться», то есть с какого-то момента начать ходить по кругу. С увеличением L свободы выбора становится меньше, чаще возникает необходимость нарушать правило запретов, но гарантий от зацикливания это всё равно не даёт. Интуитивно должно быть понятно, что чем изначально у путника больше возможных направлений движения, тем больше должно быть L. Например, если направлений всего 4 (по сторонам света: на юг, на север, на запад и на восток), то это одна ситуация, а если 8 (с добавлением юго-запада и других «диагональных» направлений), то другая. Но какой именно должна быть длина списка запретов в каждом из этих случаев, можно определить только экспериментальным путём.
Но на самом деле приведённые выше размышления наводят на мысль, что, может быть, метод вообще неработоспособен, что, возможно, в нём что-то нужно изменить?
Но на самом деле приведённые выше размышления наводят на мысль, что, может быть, метод вообще неработоспособен, что, возможно, в нём что-то нужно изменить?
А изменить есть что. Потому что до сих пор мы неявно предполагали, что длина списка исключений должна быть каким-то фиксированным числом. И действительно, в большинстве публикаций по методу направленного поиска с запретами это так и есть. Некоторые авторы для простейших случаев даже приводят эмпирические формулы расчёта оптимальной длины списка запретов в зависимости от таких параметров, как число ТС, число пунктов доставки и других (об этом можно прочитать в [2]). Но напрашивается совершенно другой путь (который в литературе тоже упоминается): если непонятно, какой именно должна быть длина списка исключений, то её надо варьировать, подбирать прямо по ходу работы алгоритма! Эта идея не только избавляет от необходимости определять длину списка запретов заранее, но и при её правильной реализации снимает проблему зацикливания! И действительно, если, к примеру, наш путник даже вернётся в какую-нибудь точку, в которой он побывал ранее, но длина списка запретов окажется не такой, как в предыдущий раз, то путник, вполне вероятно, пойдёт дальше по другому пути, поскольку в таком случае либо его прежний путь закроется правилом запретов, либо, наоборот, откроется какой-то другой путь, который был закрыт в предыдущий раз.
Но как именно следует варьировать длину списка запретов L? Самый простой способ – это заранее задать максимальную длину списка запретов Lmax, а величину L выбирать случайным образом (с помощью датчика случайных чисел) в пределах от 1 до Lmax. Это, на наш взгляд, будет уже неплохо, но, всё же, ещё не слишком «интеллектуально». На самом деле и величину Lmax тоже можно время от времени менять, причём целенаправленно: например, уменьшать, если окажется, что путнику приходится систематически нарушать правило запретов, поскольку оно слишком жёстко ограничивает свободу его передвижения. Кроме того, по достижении путником рекордной высоты имеет смысл предельно уменьшить (вообще до 1) длину списка запретов и потом постепенно её увеличивать, чтобы дать путнику возможность подольше походить вокруг, поскольку где-то поблизости может найтись ещё более высокая вершина. А если после определённого числа шагов нового рекорда высоты достигнуто не будет, то можно вернуться к случайному варьированию величины L.
Такого рода соображения, заложенные в алгоритм (а всех секретов мы, конечно, выдавать не будем), делают его поистине «высокоинтеллектуальным», гибко адаптирующимся по ходу поиска – как это обычно делает человек. Но человек в случае неудачи может вообще резко поменять стратегию поиска, выбрать совершенно другой метод. Разумеется, и в компьютерных программах такое тоже возможно. Например, к алгоритму поиска с запретами можно добавить, скажем, похожий на него, но, всё же, другой алгоритм имитации отжига и применять эти два алгоритма попеременно (если один перестаёт давать улучшения результатов – пробовать другой).
11. Так, всё-таки, реальность или красивые слова?
Сохраняя верность своему слову, мы и теперь, в конце нашего повествования, не станем навязывать читателю какой-либо ответ на этот вопрос. А лишь поделимся с ним впечатлениями наших клиентов и своими собственными о всё том же нашем планировщике перевозок комбикормов.
Клиенты, то есть реальные пользователи планировщика, после того как привыкают работать с ним, начинают отдавать должное тому, как он за считанные секунды строит планы, на составление которых у них (у людей) уходили часы. Ведь это не только освобождает их от повседневной утомительной работы, но и позволяет им планировать перевозки максимально оперативно - после получения свежей информации от автоколонн, свинокомплексов и комбикормовых заводов. А привыкание к планировщику в разных местах идёт с разной скоростью: там, где, прежде всего, диспетчерский состав посильнее, это происходит быстрее. И тогда начинают звучать требования: «Работаем только по разнарядкам планировщика!». Хотя такие требования и не всегда оправданны, поскольку иногда требуются и ручные корректировки плана (а такая возможность в нашей системе тоже имеется). Но людям (и не только диспетчерам, но и работникам свинокомплексов и комбикормовых заводов) удобнее работать по плану: предсказуемо, спокойно, без лишних опозданий и простоев, а диспетчерам не всегда хочется тратить дополнительные усилия на ручные корректировки…
А планы перевозок, выдаваемые планировщиком, выглядят порой парадоксально и даже комично.
Например, однажды (ещё на этапе тестирования системы) кто-то ошибочно ввёл в качестве расстояния от свинокомплекса до автоколонны (куда комбикормовозы возвращаются в конце смены) 3 км вместо 30-ти с лишним, и таким же малым (3 км) было там расстояние от этого же свинокомплекса до комбикормового завода. И тогда планировщик начал радостно планировать в конце смены… пустые рейсы комбикормовозов (без кормов вообще!) с завода через эту самую площадку «домой» (в автоколонну), поскольку возвращение в АК по такому маршруту (похожее на телепортацию) получалось очень быстрым, а потому – и выгодным.
Например, однажды (ещё на этапе тестирования системы) кто-то ошибочно ввёл в качестве расстояния от свинокомплекса до автоколонны (куда комбикормовозы возвращаются в конце смены) 3 км вместо 30-ти с лишним, и таким же малым (3 км) было там расстояние от этого же свинокомплекса до комбикормового завода. И тогда планировщик начал радостно планировать в конце смены… пустые рейсы комбикормовозов (без кормов вообще!) с завода через эту самую площадку «домой» (в автоколонну), поскольку возвращение в АК по такому маршруту (похожее на телепортацию) получалось очень быстрым, а потому – и выгодным.
А когда один из участников проекта (и тоже на этапе тестирования системы) в сердцах воскликнул (в адрес планировщика – прямо как живого!): «Да куда же ты поехал!», это тоже было очень забавно. А между тем, как потом выяснилось, «поехал» планировщик, как раз, куда надо, поскольку туда, куда хотел наш коллега, ехать было нельзя из-за каких-то ограничений…
12. Заключение
Надеемся, что эта наша статья понравилась читателям, поскольку сама тема очень интересна, перспективна и поистине неисчерпаема. Поэтому мы предполагаем возвращаться к ней и в дальнейшем. Но, думается, уже этот наш рассказ убедил читателей в том, что в словосочетании «искусственный интеллект», по крайней мере, что-то есть…
Между тем, планировщик перевозок комбикормов, об интеллектуальном «ядре» которого мы рассказали в этой статье, уже достаточно давно и успешно работает! Он входит в состав нашей комплексной системы по управлению перевозками «TMS 4х4» на базе технологии «ADD Cerebrum». Система разработана на платформе «1С» и включает, наряду с планированием, маршрутизацией и учётом перевозок, такие функции, как:
• Автомониторинг: контроль движения ТС по данным навигационных систем в режиме реального времени и фиксирование отклонений от нормативов (по маршрутам движения и расходу ГСМ);
• Комплексный учёт: ГСМ, шин, АКБ, запчастей, ТОиР, ДТП и штрафов, косвенных затрат;
• Интеграция с корпоративными ERP-системами и бухгалтерией, а также с датчиками уровня топлива, навигации, электронными весами;
• Расчёт ключевых логистических показателей эффективности работы автотранспортного предприятия: КТГ, КИП, экономической эффективности и качества (в разрезе подразделений и ответственны);
• И другие.
• Автомониторинг: контроль движения ТС по данным навигационных систем в режиме реального времени и фиксирование отклонений от нормативов (по маршрутам движения и расходу ГСМ);
• Комплексный учёт: ГСМ, шин, АКБ, запчастей, ТОиР, ДТП и штрафов, косвенных затрат;
• Интеграция с корпоративными ERP-системами и бухгалтерией, а также с датчиками уровня топлива, навигации, электронными весами;
• Расчёт ключевых логистических показателей эффективности работы автотранспортного предприятия: КТГ, КИП, экономической эффективности и качества (в разрезе подразделений и ответственны);
• И другие.
Закажите экономико-цифровой аудит для обоснованного решения о цифровизации
Наша команда с 2000 года занимается повышением эффективности предприятий в области оптимизации производства, логистики и цепочек поставок.
Мы выполняли проекты оптимизации процессов с Иркутской нефтяной компанией, ТНК-ВР, ТНК, Юганснефтегаз.
Нам доверяют лидеры отраслей: Норникель, Магнитогорский металлургический комбинат, КАМАЗ, Росэнергоатом, Казахмыс, Казцинк, Северсталь и многие другие. Отзывы это подтверждают.
Мы работаем по методике проведения экономико-цифрового аудита. Она проста и предназначена для выявления потерь, таких как:
1. простои производственных ресурсов,
2. необоснованные запасы,
3. различные браки и сбои,
4. повышенные затраты на разных этапах бизнес-процессов вашего предприятия.
Оформим реестр потерь и точек роста, выделим те, которые устраняются автоматизацией.
Потери не связанные с автоматизацией пойдут бонусом.
Очень важно правильно провести расчеты и представить полученную информацию руководству предприятия для принятия решения.
Наши выводы основаны на фактах: фотофакты, анализ статистики и замеров покажут реальные потери и возможности роста. Экономические эффекты в цифрах в пересчете на год. Наглядно показана окупаемость и за счет чего.
Мы привязываем наше вознаграждение к получению экономических эффектов.


