Интеллектуальное планирование производства для максимизации маржи
Л.В. Антонян, А.С. Портнов
На примере планирования производства Стеклотарного завода.
1. Вместо введения.
2. Справится ли линейное программирование?
3. Имеет ли смысл автоматизировать отдельные звенья цепочки поставок?
4. Полный перебор, случайный поиск или направленный поиск?
5. Постановка задачи.
6. Остановимся на ограничениях более подробно.
7. О формокомплектах.
8. О печах.
Краткое содержание
1. Вместо введения.
2. Справится ли линейное программирование?
3. Имеет ли смысл автоматизировать отдельные звенья цепочки поставок?
4. Полный перебор, случайный поиск или направленный поиск?
5. Постановка задачи.
6. Остановимся на ограничениях более подробно.
7. О формокомплектах.
8. О печах.
9. Несколько слов о переводах.
10. А реально ли планировать вручную?
11. Что даёт автоматизация процесса планирования?
12. Решение задачи.
13. Список исключений.
14. Правильный подход.
15. Что будет происходить с самого первого шага работы алгоритма.
16. В чём «интеллектуальность» разработанного алгоритма?
17. Длина списка исключений.
18. Заключение.
1. Вместо введения
В общем виде задачу планирования производства можно сформулировать примерно следующим образом: составить оптимальный (по заданному критерию) план-график производства заданной номенклатуры продукции в заданных объёмах и в заданные сроки при заданных ресурсных ограничениях.
Критерий оптимизации может, в частности, предполагать (и мы будем исходить именно из этого) максимизацию маржинальной прибыли (выручки от реализации продукции за вычетом прямых затрат на производство и реализацию). А ресурсные ограничения могут касаться сырья и материалов, топлива и энергии, производственных, складских и логистических мощностей, персонала и т.д.
В простейшем случае – если задача сводится к определению оптимальных объемов производства продукции и потребления соответствующих ресурсов за заданный плановых период в целом (без разнесения по времени) – возможным инструментарием её решения может быть линейное программирование.
Критерий оптимизации может, в частности, предполагать (и мы будем исходить именно из этого) максимизацию маржинальной прибыли (выручки от реализации продукции за вычетом прямых затрат на производство и реализацию). А ресурсные ограничения могут касаться сырья и материалов, топлива и энергии, производственных, складских и логистических мощностей, персонала и т.д.
В простейшем случае – если задача сводится к определению оптимальных объемов производства продукции и потребления соответствующих ресурсов за заданный плановых период в целом (без разнесения по времени) – возможным инструментарием её решения может быть линейное программирование.
2. Справится ли линейное программирование?
Во-первых, план, полученный линейным программированием, может оказаться вообще невыполнимым – как из-за «пиковых» нарушений ресурсных ограничений, так и из-за незапланированных простоев, обусловленных невозможностью надлежащей синхронизации производственных процессов.
Во-вторых, правильной целью планирования производства является, всё-таки, именно сетевой график, отражающий технологическую зависимость и последовательность выполнения операций (с конкретными сроками выполнения). Тем более что даже если в каких-то случаях технологическая зависимость операций отсутствует – например, при последовательном производстве различных видов продукции на одном и том же оборудовании – продолжительность и ресурсоёмкость процесса в целом всё равно может зависеть от порядка выполнения операций (в частности, из-за необходимых переналадок оборудования). А в такой ситуации (когда порядок важен) линейное программирование неэффективно.
Дело в том, что при сведении подобной «комбинаторной» задачи к задаче линейного программирования с неизбежностью появляются целочисленные переменные, а решение задачи линейного программирования с целочисленными переменными может потребовать непредсказуемо много машинного (компьютерного) времени. При этом за разумное время нельзя рассчитывать не только на получение наилучшего (оптимального), но и даже хоть какого-то решения, удовлетворяющего всем заданным условиям.
Разумеется, тезис о неэффективности линейного программирования как метода решения обсуждаемой задачи планирования производства относится к случаям большой размерности – когда операций, последовательность выполнения которых существенна, не 4-5, а, скажем, 40-50. Размерность задачи может быть большой и вследствие наличия альтернативных вариантов выполнения операций на нескольких различных единицах оборудования (производственных линиях, станках и т.д.), либо с использованием различных вариантов оснастки (пресс-форм, формокомплектов и т.д.).
Важно понимать, что проблема здесь не в линейном программировании как таковом, а именно в большой размерности задачи, из-за которой ни один вообще алгоритм не может гарантировать получения наилучшего (и даже хоть какого-то!) решения исходной задачи за разумное время.
Во-вторых, правильной целью планирования производства является, всё-таки, именно сетевой график, отражающий технологическую зависимость и последовательность выполнения операций (с конкретными сроками выполнения). Тем более что даже если в каких-то случаях технологическая зависимость операций отсутствует – например, при последовательном производстве различных видов продукции на одном и том же оборудовании – продолжительность и ресурсоёмкость процесса в целом всё равно может зависеть от порядка выполнения операций (в частности, из-за необходимых переналадок оборудования). А в такой ситуации (когда порядок важен) линейное программирование неэффективно.
Дело в том, что при сведении подобной «комбинаторной» задачи к задаче линейного программирования с неизбежностью появляются целочисленные переменные, а решение задачи линейного программирования с целочисленными переменными может потребовать непредсказуемо много машинного (компьютерного) времени. При этом за разумное время нельзя рассчитывать не только на получение наилучшего (оптимального), но и даже хоть какого-то решения, удовлетворяющего всем заданным условиям.
Разумеется, тезис о неэффективности линейного программирования как метода решения обсуждаемой задачи планирования производства относится к случаям большой размерности – когда операций, последовательность выполнения которых существенна, не 4-5, а, скажем, 40-50. Размерность задачи может быть большой и вследствие наличия альтернативных вариантов выполнения операций на нескольких различных единицах оборудования (производственных линиях, станках и т.д.), либо с использованием различных вариантов оснастки (пресс-форм, формокомплектов и т.д.).
Важно понимать, что проблема здесь не в линейном программировании как таковом, а именно в большой размерности задачи, из-за которой ни один вообще алгоритм не может гарантировать получения наилучшего (и даже хоть какого-то!) решения исходной задачи за разумное время.
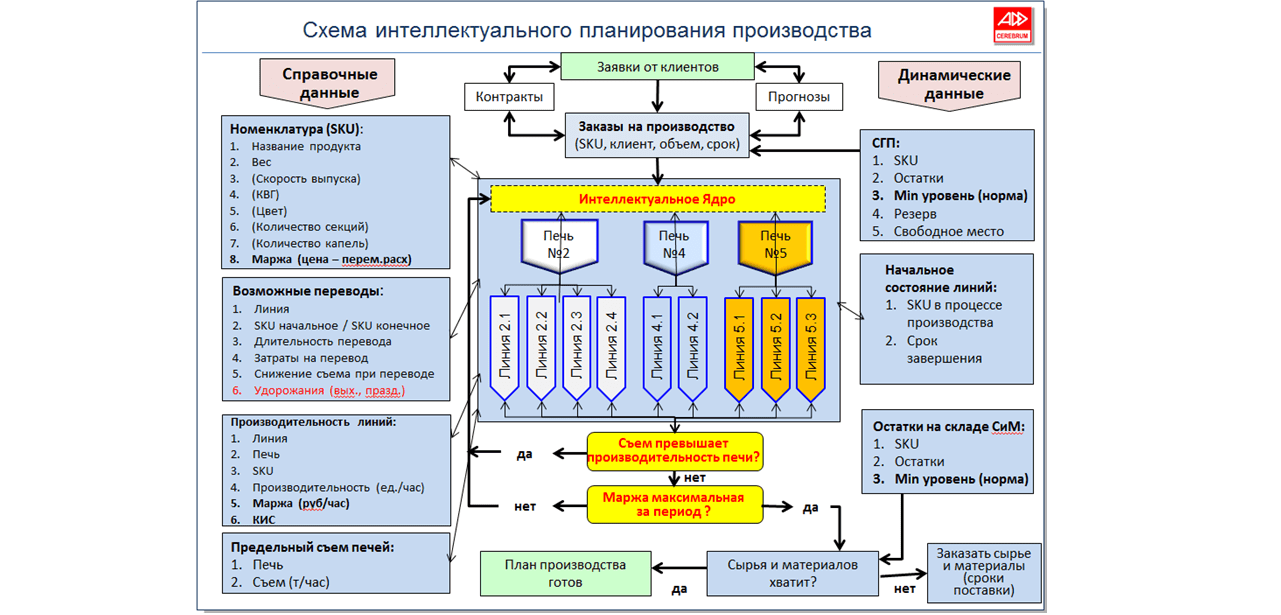
3. А может эвристика поможет?
Вообще, простейшим алгоритмом решения задач комбинаторного характера является полный перебор всех вариантов решения, но если таковых достаточно много, то полный перебор за разумное время становится невозможным, а все попытки обойти эту «невозможность» более изощрёнными методами (вроде линейного программирования) также оказываются бесперспективными. Но означает ли это, что исходная задача в принципе неразрешима?
С этим пришлось бы согласиться, если бы мы продолжали настаивать на необходимости получения наилучшего из всех возможных решений. Но как только мы откажемся от этой недостижимой цели в пользу поиска приемлемого решения, ситуация кардинальным образом изменится. Что значит «приемлемого»? Значит (в нашем случае) – обеспечивающего устраивающий нас уровень прибыльности производства. Допустим, нам удалось найти решение, дающее нам за месяц не 100 миллионов рублей маржинальной прибыли (которые мог бы обеспечить наилучший вариант плана), а «только» 99 миллионов. Разве нас это не устроило бы? Наверное, бы устроило. На самом деле мы бы даже ничего не знали о тех «оптимальных» ста миллионах (в самом деле – откуда?), но это не помешало бы нам принять полученный 99-миллионный план как приемлемый.
Таким образом, нам нужен алгоритм, на практике обеспечивающий получение приемлемого (необаятельно оптимального) решения задачи за разумное время. Такие алгоритмы принято называть эвристическими. Приведём удачное, на наш взгляд, определение эвристического алгоритма, почерпнутое нами из Википедии: Эвристический алгоритм (эвристика) — алгоритм решения задачи, включающий практический метод, не являющийся гарантированно точным или оптимальным, но достаточный для решения поставленной задачи.
Ещё там говорится, что эвристический алгоритм обычно использует различные разумные соображения, но, вообще говоря, без строгих обоснований. Последнее не должно нас смущать: важно, чтобы наш алгоритм давал приемлемые результаты и имел какие-то весомые преимущества по сравнению с другими способами решения исходной задачи, прежде всего – по сравнению с планированием производства вручную.
Но у современного компьютера есть перед человеком ряд заведомых (так сказать, «априорных») общих преимуществ – в частности, в быстродействии и в стоимости рабочего времени. На самом деле для человека задача планирования производства в полном объёме обычно оказывается вообще неподъёмной, и поэтому, чтобы сделать её мало-мальски обозримой, он (человек), как принято говорить, «пускается во все тяжкие», всеми способами пытаясь понизить размерность задачи, что ведёт к закономерному проигрышу в итоговом результате. Как именно это происходит на практике, мы расскажем далее в этой статье.
С этим пришлось бы согласиться, если бы мы продолжали настаивать на необходимости получения наилучшего из всех возможных решений. Но как только мы откажемся от этой недостижимой цели в пользу поиска приемлемого решения, ситуация кардинальным образом изменится. Что значит «приемлемого»? Значит (в нашем случае) – обеспечивающего устраивающий нас уровень прибыльности производства. Допустим, нам удалось найти решение, дающее нам за месяц не 100 миллионов рублей маржинальной прибыли (которые мог бы обеспечить наилучший вариант плана), а «только» 99 миллионов. Разве нас это не устроило бы? Наверное, бы устроило. На самом деле мы бы даже ничего не знали о тех «оптимальных» ста миллионах (в самом деле – откуда?), но это не помешало бы нам принять полученный 99-миллионный план как приемлемый.
Таким образом, нам нужен алгоритм, на практике обеспечивающий получение приемлемого (необаятельно оптимального) решения задачи за разумное время. Такие алгоритмы принято называть эвристическими. Приведём удачное, на наш взгляд, определение эвристического алгоритма, почерпнутое нами из Википедии: Эвристический алгоритм (эвристика) — алгоритм решения задачи, включающий практический метод, не являющийся гарантированно точным или оптимальным, но достаточный для решения поставленной задачи.
Ещё там говорится, что эвристический алгоритм обычно использует различные разумные соображения, но, вообще говоря, без строгих обоснований. Последнее не должно нас смущать: важно, чтобы наш алгоритм давал приемлемые результаты и имел какие-то весомые преимущества по сравнению с другими способами решения исходной задачи, прежде всего – по сравнению с планированием производства вручную.
Но у современного компьютера есть перед человеком ряд заведомых (так сказать, «априорных») общих преимуществ – в частности, в быстродействии и в стоимости рабочего времени. На самом деле для человека задача планирования производства в полном объёме обычно оказывается вообще неподъёмной, и поэтому, чтобы сделать её мало-мальски обозримой, он (человек), как принято говорить, «пускается во все тяжкие», всеми способами пытаясь понизить размерность задачи, что ведёт к закономерному проигрышу в итоговом результате. Как именно это происходит на практике, мы расскажем далее в этой статье.
4. Полный перебор, случайный поиск или направленный поиск?
Выше мы упоминали полный перебор как возможный способ поиска решения комбинаторной задачи. В чём он состоит? Есть некоторое конечное множество возможных решений рассматриваемой задачи, которые последовательно перебираются и сравниваются друг с другом с целью отыскания наилучшего из них. Относится ли полный перебор к эвристическим алгоритмам? Очевидно, нет. Потому что это абсолютно строгий алгоритм, который теоретически должен за конечное число шагов гарантированно найти наилучшее решение.
Другое дело, что практически, то есть на реально существующих вычислительных устройствах и за разумное время (а может быть, и до конца существования нашей Вселенной) он, возможно, просто не успеет завершить свою работу и, соответственно, отыскать наилучшее решение.
А вот алгоритм случайного поиска как раз является эвристическим – хотя и очень примитивным: «разумное соображение», на котором он основан, состоит в том, что коль скоро полный перебор невозможен, то лучше уж прибегнуть к случайному поиску («методом научного тыка»), тем более что его можно тем или иным образом пытаться усовершенствовать.
Наш же алгоритм относится к классу алгоритмов направленного поиска. В сущности, это тоже перебор, но который выбирает каждое следующее решение по определённому правилу, учитывающему, в частности, предшествующие результаты поиска (что, кстати, не исключает использования элементов случайности!).
Чтобы дальнейшее изложение было понятнее, мы продолжим его описанием той постановки задачи, для которой был разработан наш алгоритм, и только потом перейдём к обсуждению самого алгоритма.
Другое дело, что практически, то есть на реально существующих вычислительных устройствах и за разумное время (а может быть, и до конца существования нашей Вселенной) он, возможно, просто не успеет завершить свою работу и, соответственно, отыскать наилучшее решение.
А вот алгоритм случайного поиска как раз является эвристическим – хотя и очень примитивным: «разумное соображение», на котором он основан, состоит в том, что коль скоро полный перебор невозможен, то лучше уж прибегнуть к случайному поиску («методом научного тыка»), тем более что его можно тем или иным образом пытаться усовершенствовать.
Наш же алгоритм относится к классу алгоритмов направленного поиска. В сущности, это тоже перебор, но который выбирает каждое следующее решение по определённому правилу, учитывающему, в частности, предшествующие результаты поиска (что, кстати, не исключает использования элементов случайности!).
Чтобы дальнейшее изложение было понятнее, мы продолжим его описанием той постановки задачи, для которой был разработан наш алгоритм, и только потом перейдём к обсуждению самого алгоритма.
5. Постановка задачи
Наш алгоритм был изначально разработан для стекольного завода (производящего стеклотару: бутылки, банки, пузырьки и т.д.), однако он применим и к другим производствам (например, резинотехнических изделий). Но для наглядности мы будем в дальнейшем апеллировать к реалиям именно стекольного производства.
Итак, задан перечень производимых продуктов (изделий)
P1, P2, … , Pnp ,
каждый (каждое) из которых может производиться на одной или нескольких из имеющихся производственных линий
L1, L2, … , Lnl .
Для каждого продукта и для каждой линии известны объём (количество) и маржинальность (выручка за вычетом прямых затрат) производства за единицу времени.
Одномоментно на каждой линии может производиться только один продукт, а для перехода к производству другого продукта требуются определённые затраты времени и других ресурсов – так называемые переводы, продолжительность и стоимость которых для каждой из линий также известна.
На заданный период планирования (например, месяц или квартал) имеется перечень заявок на производство продукции
D1, D2, … , Dnd ,
каждая из которых предполагает производство заданного объёма конкретного (какого-то одного) продукта к определённому сроку (т.е. не позднее заданного момента времени).
Требуется составить график исполнения заявок, который максимизировал бы суммарную маржу за вычетом затрат на переводы с соблюдением всех ограничений: как по номенклатуре, объемам и срокам исполнения заявок, так и по производительности линий (на стекольном заводе – печей), количеству формокомплектов и другие огранияения.
Ограничения, корректность которых необходимо контролировать при составлении плана, носят глобальный характер (то есть их следует проверять не на каждой линии в отдельности, а на всех сразу).
Ну, и, конечно, главную проблему представляет размерность задачи, которая предполагается следующей:
• Количество производимых изделий (номенклатурных позиций) NP – порядка 100;
• Количество линий NL – порядка 10;
• Количество заявок ND – порядка 100.
Совершенно очевидно, что при такой размерности задачи и при таких сложных ограничениях поиск оптимального плана путем полного перебора вариантов практически невозможен, а применение случайного поиска можно представить себе только чисто теоретически.
Итак, задан перечень производимых продуктов (изделий)
P1, P2, … , Pnp ,
каждый (каждое) из которых может производиться на одной или нескольких из имеющихся производственных линий
L1, L2, … , Lnl .
Для каждого продукта и для каждой линии известны объём (количество) и маржинальность (выручка за вычетом прямых затрат) производства за единицу времени.
Одномоментно на каждой линии может производиться только один продукт, а для перехода к производству другого продукта требуются определённые затраты времени и других ресурсов – так называемые переводы, продолжительность и стоимость которых для каждой из линий также известна.
На заданный период планирования (например, месяц или квартал) имеется перечень заявок на производство продукции
D1, D2, … , Dnd ,
каждая из которых предполагает производство заданного объёма конкретного (какого-то одного) продукта к определённому сроку (т.е. не позднее заданного момента времени).
Требуется составить график исполнения заявок, который максимизировал бы суммарную маржу за вычетом затрат на переводы с соблюдением всех ограничений: как по номенклатуре, объемам и срокам исполнения заявок, так и по производительности линий (на стекольном заводе – печей), количеству формокомплектов и другие огранияения.
Ограничения, корректность которых необходимо контролировать при составлении плана, носят глобальный характер (то есть их следует проверять не на каждой линии в отдельности, а на всех сразу).
Ну, и, конечно, главную проблему представляет размерность задачи, которая предполагается следующей:
• Количество производимых изделий (номенклатурных позиций) NP – порядка 100;
• Количество линий NL – порядка 10;
• Количество заявок ND – порядка 100.
Совершенно очевидно, что при такой размерности задачи и при таких сложных ограничениях поиск оптимального плана путем полного перебора вариантов практически невозможен, а применение случайного поиска можно представить себе только чисто теоретически.
6. Остановимся на ограничениях более подробно.
Что касается ограничений по объёмам производства, то предполагается, что каждая заявка должна быть в требуемые сроки исполнена полностью, то есть что соответствующая продукция должна быть произведена в объёме, не меньшем указанного в заявке (иначе заявки следует разбивать на более мелкие с соблюдением указанного требования).
Ограничения по срокам исполнения заявок могут в нашей системе задаваться как сверху («завершить исполнения заявки не позднее указанного момента времени»), так и снизу («начать исполнение заявки не ранее указанного момента времени»). Это может быть полезно в следующих, например, ситуациях:
• если отсутствует возможность длительного хранения произведённых изделий (скажем, из-за нехватки складских площадей);
• если возможна отмена заказа (и тогда, естественно, лучше начинать производство как можно позже);
• если есть необходимость планировать остановки линий (например, на техническое обслуживание).
Ограничения по срокам исполнения заявок могут в нашей системе задаваться как сверху («завершить исполнения заявки не позднее указанного момента времени»), так и снизу («начать исполнение заявки не ранее указанного момента времени»). Это может быть полезно в следующих, например, ситуациях:
• если отсутствует возможность длительного хранения произведённых изделий (скажем, из-за нехватки складских площадей);
• если возможна отмена заказа (и тогда, естественно, лучше начинать производство как можно позже);
• если есть необходимость планировать остановки линий (например, на техническое обслуживание).
На последнем пункте имеет смысл остановиться более подробно. Чтобы, наряду с производством продукции, можно было планировать и остановки линий (на ТО или по каким-либо другим причинам), надо от узкой трактовки номенклатурного справочника как перечня производимой продукции перейти к более широкой: как перечня выполняемых работ, и тогда техническое обслуживание и другие виды работ можно будет включить туда наравне с производимыми изделиями.
7. О формокомплектах.
Формокомплект – это оснастка, необходимая для производства стеклотары или другой продукции из стекла различных форм и объёмов. Для каждого вида изделия требуется, вообще говоря, свой отдельный формокоплект, но возможны ситуации, когда:
• для производства разных изделий (например, различающихся только цветом) может использоваться один и тот же формокомплект;
• для производства одного и того же изделия в различных условиях (например, на разных линиях) могут требоваться разные формокомплекты.
В типичной ситуации у каждого изделия есть свой отдельный формокомплект, причём (ввиду дороговизны формокомплектов) – в единственном экземпляре. В такой ситуации одновременное производство одного и того же изделия на двух (и более) линиях невозможно. Но в нашей системе предусмотрен наиболее общий случай (когда каждый формокомплект может иметься в наличии в нескольких экземплярах).
• для производства разных изделий (например, различающихся только цветом) может использоваться один и тот же формокомплект;
• для производства одного и того же изделия в различных условиях (например, на разных линиях) могут требоваться разные формокомплекты.
В типичной ситуации у каждого изделия есть свой отдельный формокомплект, причём (ввиду дороговизны формокомплектов) – в единственном экземпляре. В такой ситуации одновременное производство одного и того же изделия на двух (и более) линиях невозможно. Но в нашей системе предусмотрен наиболее общий случай (когда каждый формокомплект может иметься в наличии в нескольких экземплярах).
8. О печах.
Печи производят так называемую стекломассу, из которой на линиях и производится стеклянная продукция. При этом каждая печь обеспечивает стекломассой, вообще говоря, сразу несколько подключённых к ней линий и у неё есть ограничения по производительности (называемой съёмом), причём как сверху, так и, вообще говоря, снизу, которые считаются известными.
Удельный (за единицу времени) расход стекломассы при производстве каждого из изделий на каждой из линий и при переводах также входит в перечень исходных данных.
9. Несколько слов о переводах.
Перевод – это перечень операций по смене производимого на конкретной линии изделия, основные из которых – смена формокомплекта и вывод линии на режим. Перевод требует времени (до нескольких часов) и материальных затрат (в частности, он сопровождается потерей стекломассы). Временные и материальные затраты на перевод зависят от линии и от изделий, между которыми он выполняется.
Обычно одновременно на разных линиях переводы не выполняются. Более того, обычно на каждые сутки планируют максимум один перевод, который, как правило, ставится на начало дневной смены (обычно с 8:00). При этом на выходные дни переводы, как правило, вообще не назначаются, а некоторые переводы (например, на новую или на особо сложную продукцию) не ставятся и на предвыходные дни.
В нашем алгоритме заложена гибкая схема планирования переводов, включающая возможность задания максимально допустимого числа одновременно выполняемых переводов, а также настраиваемые ограничения по дням и часам их выполнения.
10. А реально ли планировать вручную?
На первый взгляд, кажется, что уж вручную-то тем более едва ли что может получиться. Но если деваться некуда, то приходится придумывать разные ухищрения, направленные, так или иначе, на понижение размерности задачи с целью сделать её для человека обозримой.
Естественно, все эти ухищрения ведут к существенному проигрышу в итоговом результате (маржинальности плана производства) – при том, что и после них трудозатраты на получение искомого плана остаются весьма значительными. Но мы всё равно вкратце обсудим некоторые из таких приёмов, о которых нам довелось узнать от наших потенциальных клиентов, а также от программистов, которые безуспешно пытались решить рассматриваемую задачу с использованием линейного программирования (и которым очень скоро стало ясно, что без существенного понижения размерности им никак не обойтись).
Естественно, все эти ухищрения ведут к существенному проигрышу в итоговом результате (маржинальности плана производства) – при том, что и после них трудозатраты на получение искомого плана остаются весьма значительными. Но мы всё равно вкратце обсудим некоторые из таких приёмов, о которых нам довелось узнать от наших потенциальных клиентов, а также от программистов, которые безуспешно пытались решить рассматриваемую задачу с использованием линейного программирования (и которым очень скоро стало ясно, что без существенного понижения размерности им никак не обойтись).
1. Объединение заявок. Берётся несколько заявок на изготовление одного и того же изделия (и, обычно, от одного и того же клиента) и объединяются в одну (естественно, с целью уменьшения общего числа заявок). И хотя размерность задачи при этом понижается, но потенциальный результат (маржинальность) планирования, по сравнению с исходной ситуацией, вообще говоря, ухудшается. Чтобы это понять, можно прибегнуть к простой аналогии. Любой автомобилист знает, что если надо погрузить в багажник или в салон автомобиля большое количество вещей, то чем эти вещи мельче, тем плотнее (а значит, больше в суммарном объёме!) их можно разместить. А слишком большая вещь (как и слишком большая заявка) может вообще не поместиться в автомобиле (соответственно, в плане). При автоматическом же планировании производства (с помощью нашей системы) может оказаться целесообразным не объединять, а, напротив, дробить заявки, поскольку увеличение количества заявок для нашей системы не особо критично, но зато это может дать выигрыш в итоговом результате.
2. Упорядочивание заявок по срокам производства. Здесь идея состоит в том, что по срокам исполнения заявок (то есть по крайним срокам завершения производства) и по продолжительности производства определяется крайний (самый поздний) срок начала производства и при составлении плана производства в него в первоочередном порядке вставляются заявки с более ранними сроками начала производства. В результате количество вариантов резко сокращается, но и этот метод, к сожалению, ведёт к потере маржинальности – в частности, из-за возможного появления дополнительных (либо более продолжительных) переводов.
3. Минимизация количества переводов. Простейший вариант здесь – стремиться после каждой ранее поставленной в план заявки ставить заявку на то же изделие (что позволяет избежать перевода). Однако и этот приём неэффективен примерно по тем же соображениям, что и объединение заявок.
11. Что даёт автоматизация процесса планирования?
Автоматизация процесса планирования производства:
• Повышает его оперативность и качество;
• Позволяет переносить его на внерабочее время;
• Освобождает специалистов предприятия от тяжелой, трудоёмкой работы.
• Повышает его оперативность и качество;
• Позволяет переносить его на внерабочее время;
• Освобождает специалистов предприятия от тяжелой, трудоёмкой работы.
Возможность оперативного перепланирования производства, обеспечиваемая автоматизированной системой, особенно востребована:
• При согласовании производственного плана с заказчиками и исполнителями;
• При необходимости его корректировки (уже в ходе выполнения), вызванной изменениями рыночной конъюнктуры, плана продаж, условий снабжения и финансирования и т.д.;
• При возникновении аварийных ситуаций и при других внеплановых остановках производства.
• При согласовании производственного плана с заказчиками и исполнителями;
• При необходимости его корректировки (уже в ходе выполнения), вызванной изменениями рыночной конъюнктуры, плана продаж, условий снабжения и финансирования и т.д.;
• При возникновении аварийных ситуаций и при других внеплановых остановках производства.
Также важно и то, что автоматизированная система планирования производства может использоваться не только как инструмент собственно планирования, но и как средство поддержки принятия управленческих решений по развитию бизнеса, таких, как:
• Модернизация или приобретение новых печей и производственных линий;
• Закупка дополнительных формокомплектов;
• Изменение регламента выполнения переводов.
• Модернизация или приобретение новых печей и производственных линий;
• Закупка дополнительных формокомплектов;
• Изменение регламента выполнения переводов.
Здесь, прежде всего, имеется в виду возможность оценки экономического эффекта от подобных изменений путём «проигрывания» различных сценариев таких изменений. (Например, можно было бы проверить, как изменилась бы маржинальность производственного плана, если бы для наиболее востребованного рынком изделия имелся дополнительный формокомплект или если бы допускалось выполнение переводов в любое время суток и в любые дни недели.)
12. Решение задачи.
Далее по тексту «решением» (рассматриваемой задачи) мы будем называть любой производственный план, удовлетворяющий всем заданным ограничениям (по срокам исполнения заявок, формокомплектам, производительности печей, а также по переводам). А производственный план – это сетевой график распределения заявок по производственным линиям со сроками (и, тем самым, порядком) их исполнения.
При этом какие-то из заявок могут в план вообще не попасть – и тогда выручка от реализации и прямые затраты на производство продукции по этим заявкам в целевой функции вообще не учитывается. Заявкам, непопадание которых в план ведёт к существенным издержкам (в виде штрафов или потери клиентов), есть возможность присвоить статус приоритетных.
Такие (приоритетные) заявки по возможности включаются в план в первоочередном порядке. Для этого надлежащим образом модифицируется целевая функция. Но дабы не усложнять дальнейшее изложение, мы не будем учитывать этот аспект, то есть будем предполагать, что приоритетные заявки отсутствуют. Соответственно, задача будет состоять в том, чтобы из всех имеющихся заявок включить в план те, которые обеспечат его максимальную маржинальность.
Напоминаем, что в качестве целевой функции (подлежащей максимизации) берётся суммарная маржинальность плана производства, то есть выручка от реализации продукции по заявкам, включённым в план, за вычетом прямых затрат на производство и на переводы. Соответственно, при сравнении двух планов лучшим из них считается тот, у которого значение указанной целевой функции (эта самая «маржинальность») выше.
При этом какие-то из заявок могут в план вообще не попасть – и тогда выручка от реализации и прямые затраты на производство продукции по этим заявкам в целевой функции вообще не учитывается. Заявкам, непопадание которых в план ведёт к существенным издержкам (в виде штрафов или потери клиентов), есть возможность присвоить статус приоритетных.
Такие (приоритетные) заявки по возможности включаются в план в первоочередном порядке. Для этого надлежащим образом модифицируется целевая функция. Но дабы не усложнять дальнейшее изложение, мы не будем учитывать этот аспект, то есть будем предполагать, что приоритетные заявки отсутствуют. Соответственно, задача будет состоять в том, чтобы из всех имеющихся заявок включить в план те, которые обеспечат его максимальную маржинальность.
Напоминаем, что в качестве целевой функции (подлежащей максимизации) берётся суммарная маржинальность плана производства, то есть выручка от реализации продукции по заявкам, включённым в план, за вычетом прямых затрат на производство и на переводы. Соответственно, при сравнении двух планов лучшим из них считается тот, у которого значение указанной целевой функции (эта самая «маржинальность») выше.
12. Краткое описание разработанного алгоритма поиска с исключениями
Для решения рассматриваемой задачи был выбран алгоритм так называемого «поиска с исключениями» («taboo search»).
На самом деле поиск с исключениями не является законченной эвристикой, готовой к практическому применению: это некоторый метод построения законченных эвристик для конкретных задач – так называемая метаэвристика .
Метаэвристики обычно содержат параметры, управляющие их работой и требующие подбора их значений для получения эффективных эвристик, и здесь (позволим себе такой каламбур) метод поиска с исключениями – не исключение.
Общая идея поиска с исключениями заключается в том, что строится последовательность допустимых решений рассматриваемой задачи (в нашем случае – производственных планов, т.е. графиков исполнения заявок), в которой каждое следующее решение получается из предыдущего каким-нибудь элементарным преобразованием (минимальным изменением) , причём так, чтобы следующее решение было по возможности лучше предыдущего, а если улучшение невозможно, то – по возможности ненамного хуже.
Важно пояснить, что на самом деле такое список исключений, поскольку это ключевой элемент всей методики.
На самом деле поиск с исключениями не является законченной эвристикой, готовой к практическому применению: это некоторый метод построения законченных эвристик для конкретных задач – так называемая метаэвристика .
Метаэвристики обычно содержат параметры, управляющие их работой и требующие подбора их значений для получения эффективных эвристик, и здесь (позволим себе такой каламбур) метод поиска с исключениями – не исключение.
Общая идея поиска с исключениями заключается в том, что строится последовательность допустимых решений рассматриваемой задачи (в нашем случае – производственных планов, т.е. графиков исполнения заявок), в которой каждое следующее решение получается из предыдущего каким-нибудь элементарным преобразованием (минимальным изменением) , причём так, чтобы следующее решение было по возможности лучше предыдущего, а если улучшение невозможно, то – по возможности ненамного хуже.
Важно пояснить, что на самом деле такое список исключений, поскольку это ключевой элемент всей методики.
13. Список исключений.
Чтобы не возвращаться, по крайней мере, быстро, назад, к предыдущим решениям (как говорят программисты, не «зацикливаться»), эти решения (вернее, определённые их параметры) запоминаются в специальном «списке исключений» («taboo list») , и пока решение находится в списке исключений (а список исключений всё время обновляется!), возврат к нему запрещается. При этом если на конкретном шаге решение оказывается лучше всех пройденных ранее, то оно запоминается как наилучшее. Естественно, такой поиск не гарантирует отыскания абсолютно лучшего решения, но зато его можно остановить в любой момент, приняв за оптимальное наилучшее из построенных к этому моменту решений, причём чем больше времени будет выделено на поиск, тем, вообще говоря, лучше окажется найденное решение.
Если предназначение списка исключений состоит в предотвращении зацикливания, то есть возвращения в ходе итерационного процесса к решениям, полученным на предыдущих шагах, то, казалось бы, надо было бы просто запоминать все предыдущие решения и потом каждое следующее сравнивать с ними. Чисто теоретически такое возможно, но практически – совершенно нереально, поскольку для запоминания и сравнения решений потребовалось бы нереальное быстродействие компьютера, а для их хранения – столь же нереальный объём памяти. Но на самом деле такой подход не только нереалистичен, но и (по некоторым причинам, в которые мы углубляться не будем) вообще неправилен.
Если предназначение списка исключений состоит в предотвращении зацикливания, то есть возвращения в ходе итерационного процесса к решениям, полученным на предыдущих шагах, то, казалось бы, надо было бы просто запоминать все предыдущие решения и потом каждое следующее сравнивать с ними. Чисто теоретически такое возможно, но практически – совершенно нереально, поскольку для запоминания и сравнения решений потребовалось бы нереальное быстродействие компьютера, а для их хранения – столь же нереальный объём памяти. Но на самом деле такой подход не только нереалистичен, но и (по некоторым причинам, в которые мы углубляться не будем) вообще неправилен.
14. Правильный подход.
А правильный подход (который и был нами реализован) состоит в следующем. Если, допустим, на i-том шаге описанного в п.2 итерационного процесса в результате соответствующего элементарного преобразования решения какая-то j-тая заявка переместилась с k-той линии на какую-то другую (где j и k – номера заявки и линии соответственно), то мы запоминаем этот факт в специальном двумерном массиве, а затем в течение последующих n шагов, где n – длина списка исключений, мы препятствуем возвращению j-той заявки на k-тую линию (если только оно не ведет к улучшению «рекорда» маржинальности плана). В простейших вариантах алгоритма поиска с исключениями длина списка исключений обычно является параметром алгоритма – фиксированным числом, которое подбирается экспериментально.
Фиксированное число – не значит какая-то абсолютная константа (интуитивно должно быть понятно, что с увеличением размерности задачи и длина списка исключений тоже должна как-то расти); но это значит, что перед запуском итерационного процесса эта величина как-то определяется (например, по какой-то формуле) и в ходе дальнейшей работы алгоритма уже не меняется. В нашем алгоритме длина списка исключений, напротив, постоянно меняется, причём не случайным образом, а по определённым (разумным!) соображениям, которые мы обсудим в дальнейшем.
Для проверки ограничений на каждом шаге вышеописанного итерационного процесса нами была разработана универсальная схема контроля ограничений, под которую подпадают ограничения и по съёму печей, и по формокомплектам, и по переводам. В последнем случае имеется в виду контроль числа одновременно выполняемых переводов, но требовалось ещё и обеспечить соблюдение ограничений по допустимым дням и часам выполнения каждого из переводов в отдельности. Для этого был разработана отдельная процедура, которая работает следующим образом.
При вставке заявки в план выполнение предыдущей заявки (после которой должна выполняться вставляемая) при необходимости продлевается до того момента, когда возможно выполнение перевода. Например, если выполнение предыдущей заявки (в требуемом, согласно этой заявке, объёме) должно было бы завершиться в субботу, а необходимый перевод возможен только по рабочим дням с 8:00, то выполнение предыдущей заявки будет продлено до 8:00 понедельника, а возможно, и вторника, если на понедельник на какой-то другой линии уже запланирован перевод, а одновременное выполнение двух и более переводов запрещено. При этом по предыдущей заявке будет запланирован дополнительный объём выпуска продукции, который мы будем называть сверхплановым. В свою очередь, и сама вставляемая заявка может потребовать продления, если она вставляется перед какой-то другой заявкой (вставленной в план ранее). Отметим, что сверхплановые объёмы в целевой функции никак не учитываются, хотя могут быть учтены в плане производства (как в количественном, так и в денежном выражении).
Фиксированное число – не значит какая-то абсолютная константа (интуитивно должно быть понятно, что с увеличением размерности задачи и длина списка исключений тоже должна как-то расти); но это значит, что перед запуском итерационного процесса эта величина как-то определяется (например, по какой-то формуле) и в ходе дальнейшей работы алгоритма уже не меняется. В нашем алгоритме длина списка исключений, напротив, постоянно меняется, причём не случайным образом, а по определённым (разумным!) соображениям, которые мы обсудим в дальнейшем.
Для проверки ограничений на каждом шаге вышеописанного итерационного процесса нами была разработана универсальная схема контроля ограничений, под которую подпадают ограничения и по съёму печей, и по формокомплектам, и по переводам. В последнем случае имеется в виду контроль числа одновременно выполняемых переводов, но требовалось ещё и обеспечить соблюдение ограничений по допустимым дням и часам выполнения каждого из переводов в отдельности. Для этого был разработана отдельная процедура, которая работает следующим образом.
При вставке заявки в план выполнение предыдущей заявки (после которой должна выполняться вставляемая) при необходимости продлевается до того момента, когда возможно выполнение перевода. Например, если выполнение предыдущей заявки (в требуемом, согласно этой заявке, объёме) должно было бы завершиться в субботу, а необходимый перевод возможен только по рабочим дням с 8:00, то выполнение предыдущей заявки будет продлено до 8:00 понедельника, а возможно, и вторника, если на понедельник на какой-то другой линии уже запланирован перевод, а одновременное выполнение двух и более переводов запрещено. При этом по предыдущей заявке будет запланирован дополнительный объём выпуска продукции, который мы будем называть сверхплановым. В свою очередь, и сама вставляемая заявка может потребовать продления, если она вставляется перед какой-то другой заявкой (вставленной в план ранее). Отметим, что сверхплановые объёмы в целевой функции никак не учитываются, хотя могут быть учтены в плане производства (как в количественном, так и в денежном выражении).
15. Что будет происходить с самого первого шага работы алгоритма.
На первом шаге система будет пытаться включить в план какую-нибудь из заявок D1, D2, … , Dnd , то есть поставить её на какую-нибудь из линий L1, L2, … , Lnl . При этом из всех допустимых вариантов – пар (заявка, линия) – будет выбран тот, который обеспечит максимальную маржу за вычетом прямых затрат на перевод с той предплановой заявки, которая выполнялась на соответствующей линии на момент начала планового периода (не забываем и о продлении выполнения предплановой заявки, которое может при этом потребоваться!). Тем самым, системой будет поставлена в план первая из заявок. Отметим сразу, что в итоговом плане производства данная заявка, скорее всего, не останется на занятом месте, поскольку в дальнейшем перед ней могут встать какие-то другие заявки, да и она сама может впоследствии перейти на другую линию или вовсе покинуть план . Правда, последнее на следующем же шаге или в ближайшей перспективе будет не только бессмысленно, но и невозможно (пока будет фигурировать в списке исключений).
На втором шаге система, вероятно, поставит в план ещё какую-нибудь заявку, причём для неё на той линии, где оказалась первая заявка, будет два варианта: или встать после этой первой заявки, или перед ней (после предплановой) , а конкретный вариант будет выбран, как положено, по критерию максимизации маржи.
Так будет продолжаться до тех пор, пока либо вообще не останется заявок, не включённых в план, либо для части заявок на линиях не останется места. Но в обоих случаях поиск оптимального плана на этом не завершится. Более того, в обоих случаях ещё может сохраниться возможность дальнейшего увеличения маржинальности плана – в частности, путем перемещения заявок, включённых в план, между линиями. Однако рано или поздно наступит момент, когда такой возможности уже не будет (то есть любое допустимое элементарное преобразование полученного плана будет уменьшать его маржинальность).
Но и на этом поиск не завершится: дальнейшее его продолжение (уже с неизбежным временным снижением маржинальности для достижения ещё более высоких результатов в будущем) позволяет, как показали наши многочисленные тесты, получить дополнительное увеличение маржинальности ещё примерно на 20%.
На втором шаге система, вероятно, поставит в план ещё какую-нибудь заявку, причём для неё на той линии, где оказалась первая заявка, будет два варианта: или встать после этой первой заявки, или перед ней (после предплановой) , а конкретный вариант будет выбран, как положено, по критерию максимизации маржи.
Так будет продолжаться до тех пор, пока либо вообще не останется заявок, не включённых в план, либо для части заявок на линиях не останется места. Но в обоих случаях поиск оптимального плана на этом не завершится. Более того, в обоих случаях ещё может сохраниться возможность дальнейшего увеличения маржинальности плана – в частности, путем перемещения заявок, включённых в план, между линиями. Однако рано или поздно наступит момент, когда такой возможности уже не будет (то есть любое допустимое элементарное преобразование полученного плана будет уменьшать его маржинальность).
Но и на этом поиск не завершится: дальнейшее его продолжение (уже с неизбежным временным снижением маржинальности для достижения ещё более высоких результатов в будущем) позволяет, как показали наши многочисленные тесты, получить дополнительное увеличение маржинальности ещё примерно на 20%.
16. В чём «интеллектуальность» разработанного алгоритма?
Работа нашего алгоритма и в самом деле производит впечатление разумной, осмысленной деятельности. Это особенно хорошо видно в пошаговом (отладочном) режиме. Но и конечные результаты (в виде готовых планов производства) тоже вполне позволяют судить об этом. В частности, когда пытаешься понять, почему система расставила заявки так, а не иначе, то, как правило, рано или поздно обнаруживаешь разумное объяснение (см. пример о сдвиге перевода на сутки в предыдущем разделе). Интересно также наблюдать, как система реагирует на изменения исходных данных (например, при добавлении новых заявок).
Объяснение такой «интеллектуальности» получившегося алгоритма, лежащее на поверхности, состоит в том, что в его основу положена выглядящая вполне разумной стратегия поиска с исключениями .
И так оно, конечно, и есть, но, несмотря на это, первые версии нашего алгоритма оказались не слишком эффективными. И тогда мы усовершенствовали алгоритм, сделав его адаптирующимся к текущим (промежуточным) результатам поиска, то есть ещё более «интеллектуальным». Ведь как действует человек при поиске решения проблемы? Если достигнутые результаты его не удовлетворяют, он пытается что-то изменить, причём изменить осмысленно, в зависимости от ситуации, в которой он оказался. А изменить можно как количественные параметры, так и даже сам подход к решению проблемы. В нашем алгоритме глобальных изменений подхода не предусмотрено (хотя и такое вполне возможно), но определённые вариации логики поиска были реализованы. Начнём мы, однако, с параметров алгоритма.
Объяснение такой «интеллектуальности» получившегося алгоритма, лежащее на поверхности, состоит в том, что в его основу положена выглядящая вполне разумной стратегия поиска с исключениями .
И так оно, конечно, и есть, но, несмотря на это, первые версии нашего алгоритма оказались не слишком эффективными. И тогда мы усовершенствовали алгоритм, сделав его адаптирующимся к текущим (промежуточным) результатам поиска, то есть ещё более «интеллектуальным». Ведь как действует человек при поиске решения проблемы? Если достигнутые результаты его не удовлетворяют, он пытается что-то изменить, причём изменить осмысленно, в зависимости от ситуации, в которой он оказался. А изменить можно как количественные параметры, так и даже сам подход к решению проблемы. В нашем алгоритме глобальных изменений подхода не предусмотрено (хотя и такое вполне возможно), но определённые вариации логики поиска были реализованы. Начнём мы, однако, с параметров алгоритма.
17. Длина списка исключений.
Важнейшим параметром нашего алгоритма является длина списка исключений, и она, как мы уже отмечали выше, по ходу выполнения варьируется. Остановимся на этом более подробно.
Начнём с того, почему длину списка исключений в нашем случае вообще целесообразно варьировать. Во-первых, потому, что выбор конкретного фиксированного значения в нашей крайне сложной задаче было бы очень трудно обосновать .
Начнём с того, почему длину списка исключений в нашем случае вообще целесообразно варьировать. Во-первых, потому, что выбор конкретного фиксированного значения в нашей крайне сложной задаче было бы очень трудно обосновать .
Поскольку при этом важна не только размерность задачи (число линий, заявок и т.д.), но и жёсткость ограничений, зависящая от производительности печей, количества имеющихся формокомплектов и условий выполнения переводов. А если трудно выбрать конкретное значение параметра – значит, надо его варьировать! Но есть и другая причина. Варьирование длины списка исключений позволяет более надёжно застраховаться от зацикливания алгоритма, поскольку если даже на каком-то шаге итерационного процесса поиска мы вернёмся к ранее пройденному решению, то при изменившейся длине списка исключений мы, вполне вероятно, дальше (на следующем же шаге или чуть позже) пойдём другим путём.
Варьирование длины списка исключений производится случайным образом (с помощью генератора случайных чисел), но не «абы как», а из определённых соображений. Логика здесь такая. Если на каком-то шаге итерационного процесса поиска было получено наилучшее к этому моменту (рекордное по маржинальности) решение, то можно надеяться где-то «поблизости» (за несколько шагов) найти ещё более удачное решение. Но для этого надо, не удаляясь далеко от найденного решения, более тщательно поискать в его окрестности, что обеспечивается уменьшением длины списка исключений (вплоть до 1). Если же, наоборот, после отыскания последнего рекордного решения минуло большое число шагов итерационного процесса (что может даже свидетельствовать о зацикливании процесса), то надо попытаться как можно быстрее уйти подальше (в другую область множества решений), а для этого длина списка исключений должна быть большой. Большая длина списка исключений позволяет сдвинуть с места заявки, которые долгое время оставались на одном месте – в частности, самую маржинальную заявку, которая, попав в план первой, могла после этого никуда не перемещаться, или те заявки, которые до этого вообще ни разу не попадали в план.
На самом деле по ходу работы алгоритма варьируется не только сама длина списка исключений, но и (через определённое число итераций) пределы её изменения, есть и другие варьируемые параметры. Более того, в нашем алгоритме варьируются не только параметры, но (и также случайным образом) даже сама логика поиска: а именно, правило запретов и элементарные преобразования.
Резюмируя этот раздел, можно констатировать следующее: наш опыт показал, что в алгоритмах направленного поиска, подобных рассмотренному в данной статье, должно быть как можно больше варьируемых составляющих, что не только позволяет избежать зацикливания, но и повышает эффективность поиска.
Варьирование длины списка исключений производится случайным образом (с помощью генератора случайных чисел), но не «абы как», а из определённых соображений. Логика здесь такая. Если на каком-то шаге итерационного процесса поиска было получено наилучшее к этому моменту (рекордное по маржинальности) решение, то можно надеяться где-то «поблизости» (за несколько шагов) найти ещё более удачное решение. Но для этого надо, не удаляясь далеко от найденного решения, более тщательно поискать в его окрестности, что обеспечивается уменьшением длины списка исключений (вплоть до 1). Если же, наоборот, после отыскания последнего рекордного решения минуло большое число шагов итерационного процесса (что может даже свидетельствовать о зацикливании процесса), то надо попытаться как можно быстрее уйти подальше (в другую область множества решений), а для этого длина списка исключений должна быть большой. Большая длина списка исключений позволяет сдвинуть с места заявки, которые долгое время оставались на одном месте – в частности, самую маржинальную заявку, которая, попав в план первой, могла после этого никуда не перемещаться, или те заявки, которые до этого вообще ни разу не попадали в план.
На самом деле по ходу работы алгоритма варьируется не только сама длина списка исключений, но и (через определённое число итераций) пределы её изменения, есть и другие варьируемые параметры. Более того, в нашем алгоритме варьируются не только параметры, но (и также случайным образом) даже сама логика поиска: а именно, правило запретов и элементарные преобразования.
Резюмируя этот раздел, можно констатировать следующее: наш опыт показал, что в алгоритмах направленного поиска, подобных рассмотренному в данной статье, должно быть как можно больше варьируемых составляющих, что не только позволяет избежать зацикливания, но и повышает эффективность поиска.
Но есть возможность сделать алгоритм ещё более «интеллектуальным»: не просто адаптирующимся по ходу поиска, а самообучающимся! Для этого предполагается предусмотреть специальный тестовый режим его работы, в котором, в частности, подбирались бы оптимальные пределы варьирования длины списка исключений и других варьируемых параметров, а также значения параметров, не подлежащих варьированию – с тем, чтобы потом в основном режиме (при составлении реальных планов производства) алгоритм работал максимально эффективно. Но уже тема для отдельной статьи.
18. Заключение.
Современный уровень развития вычислительной техники позволяет решать задачи, которые ещё не так давно считались бы практически неразрешимыми. Такова, в частности, задача планирования производства, рассмотренная нами в данной статье. Для нас это уже не первый опыт практического применения поиска с исключениями к задачам большой размерности: у нас на базе этого похода имеются ещё и наработки по так называемой «задаче маршрутизации транспорта». Но есть и опыт применения других эвристических алгоритмов к другим задачам: в частности – алгоритма имитации отжига к «задаче коммивояжёра».
А есть ведь ещё и генетический алгоритм, алгоритм муравьиной колонии, нейронные сети!.. Подобные алгоритмы можно применять для интеллектуального планирования производства в металлургии, химпроме, пищепроме, производстве железобетонных изделий. Такой подход повышает и производительность и маржинальность производства.
Мы будем стремиться и далее углублять свой опыт применения эвристических методов, поскольку это позволяет добиваться замечательных практических результатов.
Надеемся, что наша статья была интересна самому широкому кругу читателей – включая руководителей бизнеса, для которых актуальны рассмотренные здесь задачи.
Надеемся, что наша статья была интересна самому широкому кругу читателей – включая руководителей бизнеса, для которых актуальны рассмотренные здесь задачи.

Закажите экономико-цифровой аудит для обоснованного решения о цифровизации
Наша команда с 2000 года занимается повышением эффективности предприятий в области оптимизации производства, логистики и цепочек поставок.
Мы выполняли проекты оптимизации процессов с Иркутской нефтяной компанией, ТНК-ВР, ТНК, Юганснефтегаз.
Нам доверяют лидеры отраслей: Норникель, Магнитогорский металлургический комбинат, КАМАЗ, Росэнергоатом, Казахмыс, Казцинк, Северсталь и многие другие. Отзывы это подтверждают.
Мы работаем по методике проведения экономико-цифрового аудита. Она проста и предназначена для выявления потерь, таких как:
1. простои производственных ресурсов,
2. необоснованные запасы,
3. различные браки и сбои,
4. повышенные затраты на разных этапах бизнес-процессов вашего предприятия.
Оформим реестр потерь и точек роста, выделим те, которые устраняются автоматизацией.
Потери не связанные с автоматизацией пойдут бонусом.
Очень важно правильно провести расчеты и представить полученную информацию руководству предприятия для принятия решения.
Наши выводы основаны на фактах: фотофакты, анализ статистики и замеров покажут реальные потери и возможности роста. Экономические эффекты в цифрах в пересчете на год. Наглядно показана окупаемость и за счет чего.
Мы привязываем наше вознаграждение к получению экономических эффектов.


